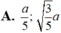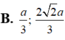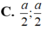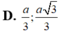Cho em hỏi: một tam giác vuông có tổng của 1 cạnh góc vuông và cạnh huyền bằng hằng số a(a>0). Khi đó diện tích lớn nhất của tam giác là?Xin cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 11 2018
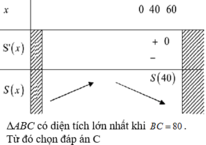
Đáp án D
Gọi độ dài một cạnh góc vuông của tam giác vuông là 
Khi đó độ dài cạnh huyền là a−x.
Độ dài cạnh góc vuông còn lại của tam giác vuông là 
Ta có diện tích tam giác vuông 
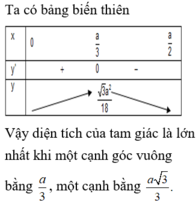
Ta có bảng biến thiên
Vậy diện tích của tam giác là lớn nhất khi một cạnh góc vuông bằng
CM
15 tháng 10 2018
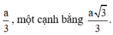
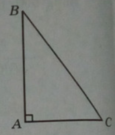
Kí hiệu cạnh góc vuông AB là x, 0 < x < a/2
Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là:
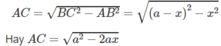
Diện tích tam giác ABC là:
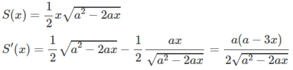
S′(x) = 0 ⇔ x = a/3
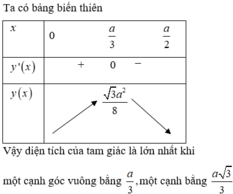
Bảng biến thiên:
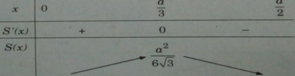
Tam giác có diện tích lớn nhất khi AB = a/3; BC = 2a/3.
CM
8 tháng 5 2018
Kí hiệu cạnh góc vuông AB là x, 0 < x < a/2
Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là:
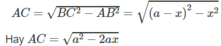
Diện tích tam giác ABC là:
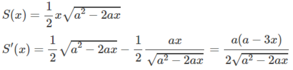
S′(x) = 0 ⇔ x = a/3
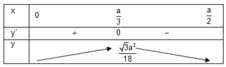
Bảng biến thiên:
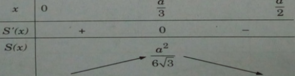
Tam giác có diện tích lớn nhất khi AB = a/3; BC = 2a/3
GV
Giáo viên Toán
Giáo viên
21 tháng 4 2017
Gọi cạnh góc vuông là \(x\) thì cạnh huyền là \(a-x\) (điều kiện: \(0< x< a-x\Leftrightarrow0< x< \dfrac{a}{2}\)) và cạnh góc vuông kia là: \(\sqrt{\left(a-x\right)^2-x^2}\).
Diện tích tam giác vuông là:
\(S=\dfrac{1}{2}x\sqrt{\left(a-x\right)^2-x^2}=\dfrac{1}{2}x\sqrt{a^2-2ax}\)
\(S'=\dfrac{1}{2}\sqrt{a^2-2ax}+\dfrac{1}{2}x\dfrac{-a}{\sqrt{a^2-2ax}}\)
\(=\dfrac{1}{2}\dfrac{a^2-3ax}{\sqrt{a^2-2ax}}\)
\(S'=0\Leftrightarrow x=\dfrac{a}{3}\)
S' đổi dấu từ dương sang âm khi x đi qua điểm \(\dfrac{a}{3}\) nên S đạt cực đại tại \(x=\dfrac{a}{3}\).
Khi đó diện tích tam giác vuông là:
\(S\left(\dfrac{a}{3}\right)=\dfrac{1}{2}\dfrac{a}{3}\sqrt{a^2-2a.\dfrac{a}{3}}=\dfrac{a^2\sqrt{3}}{18}\)
CM
7 tháng 2 2017
Đáp án A.
Giả sử cạnh góc vuông có độ dài bằng X x 0 < x < a .
Suy ra độ dài cạnh huyền là a - x .
Độ dài cạnh góc vuông còn lại là a - x 2 - x 2 = a 2 - 2 a x .
Diện tích tam giác vuông đó được tính bằng công thức S = 1 2 x . a 2 - 2 a x .
S = 1 2 a . a x . a x . a 2 - 2 a x ≤ 1 2 a . a x + a x + a 2 - 2 a x 3 3 = 1 2 a . a 6 27 = a 2 3 18 .
Dấu bằng xảy ra khi a x = a 2 - 2 a x ⇔ x = a 3 .
CM
29 tháng 9 2019
Đáp án là A.
Gọi x 0 < x < a là độ dài của một cạnh góc vuông.
Độ dài cạnh góc vuông còn lại là: a − x 2 − x 2 = a 2 − 2 a x .
Diện tích của tam giác là: S = 1 2 x a 2 − 2 a x .
Ta có S ' = 1 2 a 2 − 3 a x a 2 − 2 a x ; ⇒ S ' = 0 ⇔ x = a 3 .
Bảng biến thiên:
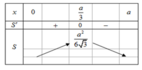
vậy S max = a 2 6 3
