Tại vị trí điểm C trên chiếc cầu CH dài 200m , người ta quan sát thấy 2 chiếc thuyền đang ở vị trí A và B . Biết góc tạo bởi AC , BC với phương vuông góc với mặt cầu tại C theo thứ tự là ACx bằng 40 độ ,BCx bằng 25 độ . Tính khoảng cách AB của 2 chiéc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
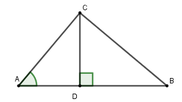
Trong tam giác BCD, góc DCB là góc tù nên là góc lớn nhất. Cạnh DB đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DB > DC (1)
Vì góc DBA là góc ngoài tại đỉnh B của tam giác BCD nên \(\widehat {ABD} > \widehat {BCD}\)nên góc DBA cũng là góc tù.
Trong tam giác ABD, góc DCA là góc tù nên là góc lớn nhất. Cạnh DA đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DA > DB (2)
Từ (1) và (2) \( \Rightarrow \) DA > DB > DC
Vậy DA dài nhất, DC ngắn nhất
Do đó, cầu thủ C gần trái bóng nhất, cầu thủ A xa trái bóng nhất.
CM
7 tháng 11 2019
Độ cao của máy bay là CD, độ dài AB = 100m. Đào đứng ở A, Mai đứng ở B
Gọi AD = x (0 < x < 100) => BD = 150 – x
Xét ACD vuông tại D, ta có CD = AD.cot A = x . c o t 45 0 = x
Xét ABD vuông tại D, ta có CD = BD.cot B = (150 – x). c o t 35 0
Nên x = (150 – x). c o t 35 0 => x ≈ 88,22 (thỏa mãn)
=> CD = x = 88,22m
Vậy độ cao của diều lúc đó so với mặt đất là 88,22m
Đáp án cần chọn là: D
CM
5 tháng 6 2019
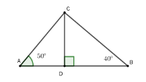
Độ cao của diều là CD, độ dài AB = 100m. Trung đứng ở A, Dũng đứng ở B
Gọi AD = x (0 < x < 100)
=> BD = 100 – x
Xét ACD vuông tại D, ta có CD = AD.tan A = x . tan 50 0
Xét ABD vuông tại D, ta có CD = BD.tan B = (100 – x). tan 40 0
Nên x . tan 50 0 = (100 – x). tan 40 0
Vậy độ cao của diều lúc đó so với mặt đất là 49,24m
Đáp án cần chọn là: B
VT
12 tháng 8 2018
Đáp án: B
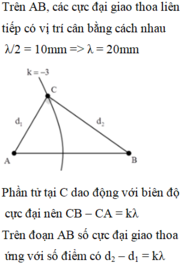
HD Giải: λ/2 = 10mm => λ = 20mm
BC lớn nhất khi C nằm trên cực đại số 3 và gần A nhất
Ta có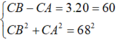 
=> CB = 67,6mm