8n:2n=4 , giúp mìk
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1./ Do 2n + 1 là số lẻ nên n2 - 2n + 4 chia hết cho 2n+1 thì 4(n2 - 2n + 4) cũng chia hết cho 2n + 1 (nhân số 4 chẵn ko tăng thêm ước cho 2n + 1)
mà: B = 4(n2 - 2n + 4) = 4n2 + 4n + 1 - 12n - 6 + 21 = (2n + 1)2 - 6(2n+1) + 21 = (2n + 1)(2n + 1 - 6) +21 = (2n + 1)(2n - 5) + 21
=> B chia hết cho 2n + 1 <=> 21 chia hết cho 2n + 1.
=> 2n + 1 thuộc U (21) = {-21;-7;-3;-1;1;3;7;21}
Khi đó n = -11; -4 ; -2; -1 ; 0 ; 1; 3 ; 10.
2./ C = 2n2 + 8n + 11 = 2n2 +4n + 4n + 8 + 3 = 2n(n + 2) + 4(n + 2) + 3 = (n + 2)(2n + 4) + 3
để 2n2 + 8n + 11 chia hết cho n + 2 thì n + 2 phải là U(3) = {-3; -1; 1; 3)
Khi đó n = -5 ; -3 ; -1 ; 1

e: \(\Leftrightarrow2n+1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{0;-1;2;-3\right\}\)

Lời giải:
Gọi $d=ƯCLN(2n+5, 8n+24)$
$\Rightarrow 2n+5\vdots d; 8n+24\vdots d$
$\Rightarrow 8n+24-4(2n+5)\vdots d$
$\Rightarrow 4\vdots d$ (1)
Vì $2n+5\vdots d$, mà $2n+5$ lẻ nên $d$ lẻ (2)
Từ $(1); (2)\Rightarrow d=1$
$\Rightarrow 2n+5, 8n+24$ nguyên tố cùng nhau.
$\Rightarrow BCNN(2n+5, 8n+24)=(2n+5)(8n+24)$

Gọi \(d=ƯC\left(8n+6;2n+1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}8n+6⋮d\\2n+1⋮d\end{matrix}\right.\) \(\Rightarrow8n+6-4\left(2n+1\right)⋮d\)
\(\Rightarrow2⋮d\Rightarrow\left\{{}\begin{matrix}d=1\\d=2\end{matrix}\right.\)
Nhưng do \(2n+1\) lẻ với mọi n nguyên \(\Rightarrow2n+1⋮̸2\) với mọi n nguyên
\(\Rightarrow d\ne2\Rightarrow d=1\) \(\Rightarrow8n+6\) và \(2n+1\) nguyên tố cùng nhau với mọi n nguyên
Hay \(\dfrac{8n+6}{2n+1}\) là phân số tối giản với mọi n nguyên


\(\Rightarrow2^{3n-n}=16=2^4\Rightarrow2n=4\Rightarrow n=2\)
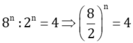
8n:2n=4
=> (8:2)n=4
=> 4n=41
=> n=1
\(8^n:2^n=4\)
\(\left(8:2\right)^n=4\)
\(4^n=4=4^1\)
Vậy n = 1