Trong hình 1, biết
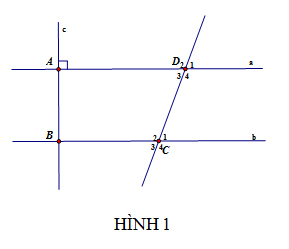
∠D1 = 700 , ∠C2 = 110
, c⊥a.
a/ Chứng minh: a//b
b/ Chứng minh: c⊥b
giúp mk với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
2
8 tháng 12 2016
Ta có: \(\widehat{C_1}\)+\(\widehat{C_2}\)=1800 (kề bù)
hay \(\widehat{C_1}\)+1100 = 1800
=> \(\widehat{C_1}\)= 1800 - 1100 = 700
Ta có: \(\widehat{C_1}\)=\(\widehat{D_1}\)=700
Mà \(\widehat{C_1}\); \(\widehat{D_1}\) :đồng vị
=> a // b
Ta có: a // b; a\(\perp\)c
=> b \(\perp\) c hay c \(\perp\)b (đpcm)
17 tháng 10 2021
a, Vì m và n cùng vuông góc với a nên m//n
b, Vì m//n nên \(\widehat{B_1}=\widehat{D_1}=70^0\left(so.le.trong\right);\widehat{B_1}=\widehat{D_2}=70^0\left(đồng.vị\right)\)
c, Vì \(\widehat{B_1}+\widehat{G_1}=70^0+110^0=180^0\) mà 2 góc này ở vị trí trong cùng phía nên p//n
Mà n⊥a nên p⊥a
17 tháng 11 2021
\(\widehat{B}=\dfrac{180^0-\widehat{A}}{2}=35^0\)
\(\left\{{}\begin{matrix}\widehat{B}+\widehat{ABD}+\widehat{BAD}=180^0\\\widehat{C}+\widehat{ACD}+\widehat{CAD}=180^0\end{matrix}\right.\)
Mà \(\widehat{B}=\widehat{C};\widehat{ADB}=\widehat{ADC}=90^0\)
Vậy \(\widehat{BAD}=\widehat{CAD}\) hay AD là p/g \(\widehat{BAC}\)
NT
2
4 tháng 10 2021
a) Ta có: \(\widehat{D_1}+\widehat{D_2}=180^0\)(kề bù)
\(\Rightarrow\widehat{D_1}=180^0-110^0=70^0\)
\(\Rightarrow\widehat{D_1}=\widehat{C_1}=70^0\)
Mà 2 góc này đồng vị
=> a//b
b) Ta có: a//b,a⊥c
=> c⊥b(từ vuông góc đến song song)
NT
2
12 tháng 1 2022
\(\dfrac{a}{b}=\dfrac{b}{c}\Rightarrow ac=b^2\)
\(\dfrac{a^2+b^2}{b^2+c^2}=\dfrac{a^2+ac}{ac+c^2}=\dfrac{a\left(a+c\right)}{c\left(a+c\right)}=\dfrac{a}{c}\)
trc hết D1= 70O
a) D1 = D3= 70 (đối đỉnh)
C2 + D3 = 110+70 = 180 ( 2 góc này ở
vị trí trong cùng phía) nên a//b
b) theo a) có a//b
mà c vuông góc với a => c vuong goc voi b