chứng minh đa thức sau luôn dương với mọi giá trị của x
x^4-x^3+3x^2-2x+2
vẫn thế sao chả hiểu lổi cái dạng này ý nhỉ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 12 2016
a)2x(2x+7)=4(2x+7)
2x(2x+7)-4(2x+7)=0
(2x+7)(2x-4)=0
\(\Rightarrow\orbr{\begin{cases}2x+7=0\\2x-4=0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=-\frac{7}{2}\\x=2\end{cases}}\)
5 tháng 12 2016
b)Ta có:x3-4x2+ax=x3-3x2-x2+ax
=x2(x-3)-x(x-a)
Để x3-4x2+ax chia hết cho x-3 thì a=3
11 tháng 9 2020
Bài 1.
( 1 - 3x )( x + 2 )
= 1( x + 2 ) - 3x( x + 2 )
= x + 2 - 3x2 - 6x
= -3x2 - 5x + 2
= -3( x2 + 5/3x + 25/36 ) + 49/12
= -3( x + 5/6 )2 + 49/12 ≤ 49/12 ∀ x
Đẳng thức xảy ra <=> x + 5/6 = 0 => x = -5/6
Vậy GTLN của biểu thức = 49/12 <=> x = -5/6
Bài 2.
A = x2 + 2x + 7
= ( x2 + 2x + 1 ) + 6
= ( x + 1 )2 + 6 ≥ 6 > 0 ∀ x
=> A vô nghiệm ( > 0 mà :)) )
Bài 3.
M = x2 + 2x + 7
= ( x2 + 2x + 1 ) + 6
= ( x + 1 )2 + 6 ≥ 6 > 0 ∀ x
=> đpcm
Bài 4.
A = -x2 + 18x - 81
= -( x2 - 18x + 81 )
= -( x - 9 )2 ≤ 0 ∀ x
=> đpcm
Bài 5. ( sửa thành luôn không dương nhé ;-; )
F = -x2 - 4x - 5
= -( x2 + 4x + 4 ) - 1
= -( x + 2 )2 - 1 ≤ -1 < 0 ∀ x
=> đpcm
XO
11 tháng 9 2020
Bài 2
Ta có A = x2 + 2x + 7 = (x2 + 2x + 1) + 6 = (x + 1)2 + 6\(\ge\)6 > 0
Đa thức A vô nghiệm
Bại 3: Ta có M = x2 + 2x + 7 = (x2 + 2x + 1) + 6 = (x + 1)2 + 6\(\ge\)6 > 0 (đpcm)
Bài 4 Ta có A = -x2 + 18x - 81 = -(x2 - 18x + 81) = -(x - 9)2 \(\le0\)(đpcm)
Bài 5 Ta có F = -x2 - 4x - 5 = -(x2 + 4x + 5) = -(x2 + 4x + 4) - 1 = -(x + 2)2 - 1 \(\le\)-1 < 0 (đpcm)
CM
5 tháng 7 2018
Điều kiện x ≠ 1 và x ≠ - 1
Ta có:
Biểu thức dương khi x 2 + 2 x + 3 > 0
Ta có: x 2 + 2 x + 3 = x 2 + 2 x + 1 + 2 = x + 1 2 + 2 > 0 với mọi giá trị của x.
Vậy giá trị của biểu thức dương với mọi giá trị x ≠ 1 và x ≠ - 1
1 tháng 8 2023
a: Sửa đề: 1/4x+x^2+2
x^2+1/4x+2
=x^2+2*x*1/8+1/64+127/64
=(x+1/8)^2+127/64>=127/64>0 với mọi x
=>ĐPCM
b: 2x^2+3x+1
=2(x^2+3/2x+1/2)
=2(x^2+2*x*3/4+9/16-1/16)
=2(x+3/4)^2-1/8
Biểu thức này ko thể luôn dương nha bạn
c: 9x^2-12x+5
=9x^2-12x+4+1
=(3x-2)^2+1>=1>0 với mọi x
d: (x+2)^2+(x-2)^2
=x^2+4x+4+x^2-4x+4
=2x^2+8>=8>0 với mọi x
LA
4
TA
18 tháng 5 2021
`x^4+2x^2+1`
`=(x^2)^2 + 2.x^2 .1 + 1^2`
`=(x^2+1)^2 > 0 forall x`.
23 tháng 6 2017
a)
\(=x^2+2.1,5x+1.5^2+0,75\)
\(=\left(x+1.5\right)^2+0,75\)
Vì (x+1.5)^2 luôn dương và 0,75 dương nên biểu thức luôn dương
b)
\(=x^2+2x+1+y^2-4y+4+1\)
\(=\left(x+1\right)^2+\left(y-2\right)^2+1\)
Lập luận tương tự câu a), được biểu thức luôn dương
c)
\(=x^2+2xy+y^2+x^2-2x+1+1\)
\(=\left(x+y\right)^2+\left(x-1\right)^2+1\)
Lập luận tương tự
CM
10 tháng 7 2018
Điều kiện x ≠ 0 và x ≠ -3
Ta có:
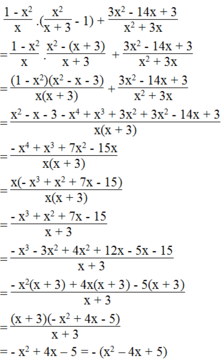
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
23 tháng 9 2021
\(E=x^2+2x+15=\left(x^2+2x+1\right)+14=\left(x+1\right)^2+14\ge14>0\forall x\)
17 tháng 9 2021
a)\(A=x^2+x+1=\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\)
b) \(B=2x^2+2x+1=2\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{1}{2}=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{2}\ge\dfrac{1}{2}>0\)
x4 - x3 + 3x2 - 2x + 2
= x4 - x3 + x2 + 2x2 - 2x + 2
= x2(x2 - x + 1) + 2(x2 - x + 1)
= (x2 + 2)(x2 - x + 1)
= (x2 + 2)(x2 - x + 1/4 + 3/4)
= (x2 + 2)[(x - 1/2)2 + 3/4]
x2 + 2 lớn hơn hoặc bằng 2
(x - 1/2)2 + 3/4 lớn hoăn hoặc bằng 3/4
(x2 + 2)[(x - 1/2)2 + 3/4] lớn hơn hoặc bằng 3/2 > 0 (đpcm)