Question

[Lê Thị Hà]

    Bài tập : 
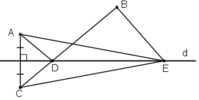
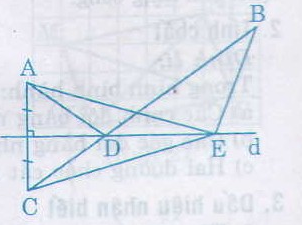
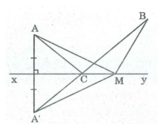
a) Cho hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng d (h.60). Gọi C là điểm đối xứng với A qua d. Gọi D là giao điểm của đường thẳng d và đoạn thẳng BC. Gọi E là điểm bất kì của đường thẳng d (E khác D).

Chứng minh rằng AD + DB < AE + EB.

b) Bạn Tú đang ở vị trí A, cần đến bờ sông d lấy nước rồi đi đến vị trí B (h.60). Con đường ngắn nhất mà bạn Tú nên di là con đường nào ?

Answer 1

[Khánh Hà]

Bài giải:        

a) Ta có AD = CD

nên AD + DB = CD  + DB = CB      (1)                                     

và AE = CE                              

  nên AE + EB = CE + EB               (2)

mà CB < CE + EB                           (3)

Nên từ (1) (2) và (3), suy ra

AD + DB < AE + EB

b) Theo câu a con đường ngắn nhất mà bạn Tú phải đi là con đường ADB.