giúp m vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 9 2021
Xét ΔIDK vuông tại D và ΔIDC vuông tại D có
ID chung
DK=DC
Do đó: ΔIDK=ΔIDC
Suy ra: \(\widehat{KID}=\widehat{DIC}\)
mà \(\widehat{KID}=\widehat{AIB}\)
nên \(\widehat{AIB}=\widehat{DIC}\)
31 tháng 1 2023
Xet ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=OB/OD
=>CE/DE=DF/CF
=>\(\dfrac{CF+FE}{DE}=\dfrac{DE+EF}{CF}\)
=>\(CF^2+FE\cdot CF=DE^2+DE\cdot FE\)
=>(CF-DE)(CF+DE)-FE(CF-DE)=0
=>(CF-DE)(CF+DE-FE)=0
=>CF=DE
5 tháng 4 2022
\(\Leftrightarrow\dfrac{90}{x}-\dfrac{90}{x+5}=\dfrac{1}{5}\)
\(\Leftrightarrow x\left(x+5\right)=450x+2250-450x\)
\(\Leftrightarrow x^2+5x-2250=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=45\\x=-50\end{matrix}\right.\)
5 tháng 4 2022
ĐKXĐ: \(x\ne0;x\ne-5\)
\(\dfrac{180}{x}-\dfrac{180}{x+5}=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{180.5.\left(x+5\right)}{5x\left(x+5\right)}-\dfrac{180.5.x}{5x\left(x+5\right)}=\dfrac{2.x.\left(x+5\right)}{5x\left(x+5\right)}\)
\(\Leftrightarrow900x+4500-900x=2x^2+10x\)
\(\Leftrightarrow2x^2+10x-4500=0\)
\(\Leftrightarrow x^2+5x-2250=0\)
\(\Leftrightarrow x^2+50x-45x-2250=0\)
\(\Leftrightarrow x\left(x+50\right)-45\left(x+50\right)=0\)
\(\Leftrightarrow\left(x+50\right)\left(x-45\right)=0\)
=> x+50=0 hoặc x-45=0
x=-50 x=45
Vậy....
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
\(y'=\left(m-1\right)x^2+2mx+3m-2\)
Với \(m=1\) ko thỏa mãn
\(y'>0\) ; \(\forall x\in R\) khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1>0\\\Delta'=m^2-\left(3m-2\right)\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\2m^2-5m+2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left[{}\begin{matrix}m>2\\m< \dfrac{1}{2}\\\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow m>2\)
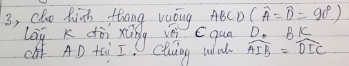
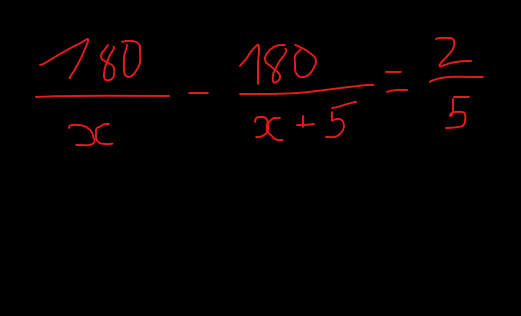
MN là đường trung bình tam giác ABC \(\Rightarrow\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{BC}\)
NP là đường trung bình tam giác ABC \(\Rightarrow\overrightarrow{NP}=\dfrac{1}{2}\overrightarrow{AB}\Leftrightarrow\overrightarrow{AB}=2\overrightarrow{NP}\Leftrightarrow\overrightarrow{BA}=-2\overrightarrow{NP}\)
MP là đường trung bình \(\Rightarrow\overrightarrow{MP}=\dfrac{1}{2}\overrightarrow{AC}\)
Mà N là trung điểm AC \(\Rightarrow\overrightarrow{NA}=\dfrac{1}{2}\overrightarrow{CA}=-\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{MP}=-\overrightarrow{NA}\)
3.
\(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|=\left|\overrightarrow{BD}\right|=BD=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\left|\overrightarrow{u}\right|=\left|2\overrightarrow{AD}-\overrightarrow{BA}\right|\Rightarrow\left|\overrightarrow{u}\right|^2=\left(2\overrightarrow{AD}-\overrightarrow{BA}\right)^2=4AD^2+BA^2-4\overrightarrow{AD}.\overrightarrow{BA}\)
\(=4AD^2+BA^2=5a^2\Rightarrow\left|\overrightarrow{u}\right|=a\sqrt{5}\)
\(\left|\overrightarrow{CD}-2\overrightarrow{BO}\right|=\left|\overrightarrow{CD}-\overrightarrow{BD}\right|=\left|\overrightarrow{CD}+\overrightarrow{DB}\right|=\left|\overrightarrow{CB}\right|=a\)