1 tháng máy có khoảng cách giữa trần và sàn là 2,7 m bắt đầu từ mặt đất chuyển động hướng đi lên với gia tốc không đổi là 1,2 m. Khi thành máy xuất phát được 2s thì 1 chiếc bulông ở trên trần thang máy rơi xuống . Hãy xác định khoảng thời gian từ lúc bulông rời sàn cho đến khi chạm sàn thang máy và độ dời của bulông trong khoảng thời gian trên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
18 tháng 1 2019
Chọn A.
Chọn hệ quy chiếu gắn với mặt đất, chọn gốc tọa độ là một điểm ngang bằng với sàn A, chọn t = 0 tại thời điểm vật bắt đầu rơi thì phương trình chuyển động của của sàn là:
y = 2,4t + t 2
và của vật là:
y = 2,47 + 2,4t + 0,5g t 2
= 2,47 + 2,4t - 5 t 2
(Gia tốc có dấu âm vì chuyển động của vật là đi lên chậm dần đều với vận tốc ban đầu là v 0 = 2,4m/s)
Vật chạm sàn sau thời gian t là nghiệm của phương trình :
2,47 + 2,4t - 5 t 2 = 2,4t + t 2
Giải ra và loại nghiệm âm ta được t = 0,64s.
VT
27 tháng 8 2019
Đáp án B
Chọn trục tọa độ Ox có chiều trùng cới chiều chuyển động của người đi xe máy và xe buýt, chiều dương hướng từ người đi xe máy đến xe buýt. Gốc O tại vị trí xuất phát của người đi xe máy. Gốc thời gian là lúc người và xe buýt bắt đầu chuyển động.
Tại thời điểm t:
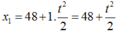
Vị trí của xe buýt :
Vị trí của người đi xe máy:
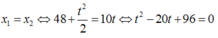
Khi người đi xe máy bắt kị xe buýt thì
Như vật thời gian nhỏ nhất để người đi xe máy bắt kịp xe buýt là 8 s, sau đó người đi xe máy sẽ vượt lên xe buýt. Tại t2 = 12s xe buýt sẽ lại đuổi kịp xe máy. Sau thời điểm này, xe buýt luôn ở trước xe máy.
VT
5 tháng 2 2019
Chọn A.
Chọn hệ quy chiếu gắn với mặt đất, chọn gốc tọa độ là một điểm ngang bằng với sàn A, chọn t = 0 tại thời điểm vật bắt đầu rơi thì phương trình chuyển động của của sàn là:
y = 2,4t + t2
và của vật là: y = 2,47 + 2,4t + 0,5gt2 = 2,47 + 2,4t - 5t2
(Gia tốc có dấu âm vì chuyển động của vật là đi lên chậm dần đều với vận tốc ban đầu là v0 = 2,4m/s)
Vật chạm sàn sau thời gian t là nghiệm của phương trình :
2,47 + 2,4t - 5t2 = 2,4t + t2
Giải ra và loại nghiệm âm ta được t = 0,64s.
VT
4 tháng 10 2018
Đáp án A
Chọn hệ quy chiếu gắn với mặt đất, chọn gốc tọa độ là một điểm ngang bằng với sàn A, chọn t = 0 tại thời điểm vật bắt đầu rơi thì phương trình chuyển động của của sàn là:
y = 2,4t + t2
và của vật là: y = 2,47 + 2,4t + 0,5gt2 = 2,47 + 2,4t - 5t2
(Gia tốc có dấu âm vì chuyển động của vật là đi lên chậm dần đều với vận tốc ban đầu là v0 = 2,4m/s)
Vật chạm sàn sau thời gian t là nghiệm của phương trình:
2,47 + 2,4t - 5t2 = 2,4t + t2
Giải ra và loại nghiệm âm ta được t = 0,64s
VT
6 tháng 12 2019
Đáp án B
Hướng dẫn:
Ta có thể quy bài toán con lắc lò xo trong thang máy chuyển động với gia tốc về trường hợp con lắc chịu tác dụng của trường lực ngoài F → = F q t → = − m a → .
Để đơn giản, ta có thể chia chuyển động của con lắc thành hai giai đoạn:
Giai đoạn 1: Thang máy chuyển động nhanh dần đều đi lên, con lắc dao động điều hòa quanh vị trí cân bằng mới O′.
Dưới tác dụng của lực quán tính ngược chiều với gia tốc, vị trí cân bằng mới O′ của con lắc nằm phía dưới vị trí cân bằng cũ O một đoạn O O ' = m a k = 0 , 4.4 100 = 1 , 6 cm.
+ Biến cố xảy ra không làm thay đổi tần số góc của dao động ω = k m = 100 0 , 4 = 5 π rad/s → T = 0,4 s.
Thời điểm thang máy bắt đầu chuyển động, vật ở biên trên, do vậy sau khoảng thời gian Δt = 12,5T = 5 s vật sẽ đến vị trí biên dưới, cách vị trí cân bằng cũ O một đoạn 2OO′ = 3,2 cm.
Giai đoạn 2: Thang máy chuyển động thẳng đều, con lắc dao động điều hòa quanh vị trí cân bằng O.
+ Thang máy chuyển động thẳng đều → a = 0, không còn lực quán tính nữa vị trí cân bằng bây giờ trở về O.
→ Con lắc sẽ dao đông với biên độ mới A′ = 2OO′ = 3,2 cm.
→ Thế năng đàn hồi của con lắc cực đại khi con lắc ở biên dưới, tại vị trí này lò xo giãn Δ l m a x = A ' + m g k = 3 , 2 + 0 , 4.10 100 = 7 , 2 cm.
+ Thế năng đàn hồi cực đại E d h m a x = 1 2 k Δ l m a x 2 = 1 2 .100 0 , 072 2 ≈ 0 , 26 J.
