x^2+2xy+y^2-xz-zy giúp tớ nha mấy bạn mai mình nộp cho cô thanks bạn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ST
1
Những câu hỏi liên quan
9 tháng 10 2016
\(\left(x+2\right)\left(x-2\right)-x\left(x-3\right)\)
\(=x^2-4-x^2+3x=3x-4\)
9 tháng 7 2018
\(\left(X^2+2x+1\right)+\left(4y^2+\frac{4.1y}{4}+\frac{1}{16}\right)+2-\frac{1}{16}.\)
\(\left(x+1\right)^2+\left(2y+\frac{1}{4}\right)^2+\frac{15}{16}\ge\frac{15}{16}\)
9 tháng 7 2018
\(x^2+4y^2+2x-y+2\)
\(=\left(x^2+2x+1\right)+\left[\left(2y\right)^2-2.2y.\frac{1}{4}+\left(\frac{1}{4}\right)^2\right]+\frac{15}{16}\)
\(=\left(x+1\right)^2+\left(2y-\frac{1}{4}\right)+\frac{15}{16}\)
Ta có: \(\hept{\begin{cases}\left(x+1\right)^2\ge0\forall x\\\left(2y-\frac{1}{4}\right)\ge0\forall y\end{cases}\Rightarrow\left(x+1\right)^2+\left(2y-\frac{1}{4}\right)+\frac{15}{16}\ge\frac{15}{16}}\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)^2=0\\\left(2y-\frac{1}{4}\right)=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+1=0\\2y-\frac{1}{4}=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-1\\y=\frac{1}{8}\end{cases}}}\)
Vậy GTNN của \(x^2+4y^2+2x-y+2=\frac{15}{16}\Leftrightarrow\hept{\begin{cases}x=-1\\y=\frac{1}{8}\end{cases}}\)
Tham khảo nhé~
LT
2
HP
27 tháng 3 2016
xy+x-2y=5
<=>xy-2y+x=5
<=>y(x-2)+x-2=5-2
<=>y(x-2)+(x-2)=3
<=>(y-1)(x-2)=3
tới đây tự làm tiếp
27 tháng 3 2016
Ta có: x.y+x-2y = 5
=> x.(y+1)-2y = 5
=> x.(y+1)-2y-2 = 3
=> x.(y+1)-2.(y+1) = 3
=> (x-2).(y+1) = 3
Lập bảng tìm x;y
| x - 2 | -3 | -1 | 1 | 3 |
| y + 1 | -1 | -3 | 3 | 1 |
| x | -1 | 1 | 3 | 5 |
| y | -2 | -4 | 2 | 0 |
Vậy x; y là: (-1;-2);(1;-4);(3;2);(5;0)
C
4 tháng 1
a) y x 5 = 1948 + 247
y x 5 = 2195
y = 2195 : 5
y = 439
b) y : 3 = 190 - 90
y : 3 = 100
y = 100 x 3
y = 300
c) y - 8357 = 3829 x 2
y - 8357 = 7658
y = 7658 + 8357
y = 16 015
d) y x 8 = 182 x 4
y x 8 = 728
y = 728 : 8
y = 91
LT
4 tháng 1
a) y x 5 = 1948 + 247
y x 5 = 2195
y = 2195 :5
y = 439
b) y : 3 = 190 - 90
y : 3 = 100
y = 100 x 3
y = 300
c) y - 8357 = 3829 x 2
y - 8357 = 7658
y = 7658 + 8357
y = 16015
d) y x 8 = 182 x 4
y x 8 = 728
y = 728 : 8
y = 91
23 tháng 4 2018
Ta có :
\(A=\frac{x^2+x+1}{\left(x+1\right)^2}\)
\(A=\frac{x^2+2x+1-x-1+1}{x^2+2x+1}\)
\(A=\frac{x^2+2x+1}{\left(x+1\right)^2}+\frac{-x-1}{\left(x+1\right)^2}+\frac{1}{\left(x+1\right)^2}\)
\(A=\frac{\left(x+1\right)^2}{\left(x+1\right)^2}-\frac{x+1}{\left(x+1\right)^2}+\frac{1^2}{\left(x+1\right)^2}\)
\(A=1-\frac{1}{x+1}+\left(\frac{1}{x+1}\right)^2\)
Đặt \(a=\frac{1}{x+1}\) ta có :
\(A=1-a+a^2\)
\(A=a^2-a+1\)
\(A=\left(a^2-a+\frac{1}{4}\right)+\frac{3}{4}\)
\(A=\left(a-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Dấu "=" xảy ra khi và chỉ khi \(\left(a-\frac{1}{2}\right)^2=0\)
\(\Leftrightarrow\)\(a-\frac{1}{2}=0\)
\(\Leftrightarrow\)\(a=\frac{1}{2}\)
Do đó :
\(a=\frac{1}{x+1}\)
\(\Leftrightarrow\)\(\frac{1}{2}=\frac{1}{x+1}\)
\(\Leftrightarrow\)\(x+1=2\)
\(\Leftrightarrow\)\(x=1\)
Vậy GTNN của \(A\) là \(\frac{3}{4}\) khi \(x=1\)
Chúc bạn học tốt ~
HN
1
KV
29 tháng 10 2023
1) 43 . 78 - 43 . 48 + 30 . 80 - 30 . 23
= 43.(78 - 48) + 30.(80 - 23)
= 43.30 + 30.57
= 30.(43 + 57)
= 30.100
= 3000
2) 31.175 - 31.50 + 69.125
= 31.(175 - 50) + 69.125
= 31.125 + 69.125
= 125.(31 + 69)
= 125.100
= 12500
3) 2.[(7 - 3¹³ : 3¹²) : 2² + 99] - 10²
= 2.[(7 - 3) : 4 + 99] - 100
= 2.(4 : 4 + 99) - 100
= 2.(1 + 99) - 100
= 2.100 - 100
= 200 - 100
= 100
4) 2²⁰¹⁹.2² : 2²⁰¹⁶ - 125 : 5² + 2019⁰
= 2²⁰²¹ : 2²⁰¹⁶ - 125 : 25 + 1
= 2⁵ - 5 + 1
= 32 - 4
= 28
12 tháng 10 2021
\(2x^2+y^2+2x-2xy+5-4y=0\)
\(\Leftrightarrow\left[y^2-2y\left(x+2\right)+\left(x+2\right)^2\right]+\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow\left(y-x-2\right)^2+\left(x-1\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y-x-2=0\\x-1=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
\(S=\left(x+2\right)^2+\left(y-1\right)^2=\left(1+2\right)^2+\left(3-1\right)^2\)
\(=3^2+2^2=13\)
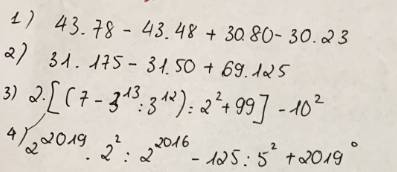
\(x^2+2xy+y^2-xz-zy\)
\(=\left(x+y\right)^2-z\left(x+y\right)\)
\(=\left(x+y\right)\left(x+y-z\right)\)