Giúp vs mn ơi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



THAM KHẢO
Gọi x là v.tốc dự định của xe(x>0, km/h)
Nửa quãng đường xe đi là: 120:2=60(km)
=> Vận tốc đi nửa quãng đường là: 60x60x (km/h)
=> Thời gian đi dự định là: 120x(h)120x(h)
Vì nửa qquangx đường sau xe đi với thời gian là: 60x+10(h)60x+10(h)
Theo bra ta có:
60x+60x+10=120x−0.560x+60x+10=120x−0.5
Gải được x=40(tmđk)
Vậy v.tốc dự định là 40km/h

a: =>12x+5(x-1)=100-10(3x-1)
=>12x+5x-5=100-30x+30
=>17x-5=-30x+130
=>47x=135
=>x=135/47
b: \(\Leftrightarrow6\left(2x-1\right)+2\left(5-x\right)=24-9\left(x+1\right)\)
=>12x-6+10-2x=24-9x-9
=>10x+4=-9x+15
=>19x=11
=>x=11/19

Bài 1.
a.
\(A=\frac{5}{4}(-8).(x^2.x)(y^2.y^2)=-10x^3y^4\)
b. $A=-10.1^3.(-1)^4=-10$
2.
\(B=\frac{15}{2}(\frac{1}{3})^2-\frac{5}{2}(\frac{1}{3})=0\)
Bài 2:
a.
$f(x)=(5x^3-2x^3)+(x^2+3x^2)-2x-3$
$=3x^3+3x^2-2x-3$
$g(x)=(2x^4-2x^4)+(-5x^3+7x^3)+(6x-4x)-1$
$=2x^3+2x-1$
b.
$f(x)+g(x)=(3x^3+3x^2-2x-3)+(2x^3+2x-1)$
$=5x^3+3x^2-4$
c.
$f(x)-g(x)=(3x^3+3x^2-2x-3)-(2x^3+2x-1)$
$=x^3+3x^2-4x-2$

\(A=\left(\dfrac{x+2}{x-1}-\dfrac{2x+3}{2x+1}\right):\left(1-\dfrac{x-2}{x-1}\right)\)
\(A=\left(\dfrac{\left(x+2\right)\left(2x+1\right)-\left(2x+3\right)\left(x-1\right)}{\left(x-1\right)\left(2x+1\right)}\right):\left(\dfrac{x-1-x+2}{x-1}\right)\)
\(A=\dfrac{2x^2+4x+x+2-\left(2x^2+3x-2x-3\right)}{\left(x-1\right)\left(2x+1\right)}.\left(x-1\right)\)
\(A=\dfrac{4x+5}{2x+1}\)
Lần sau đăng bên box Toán nha bạn



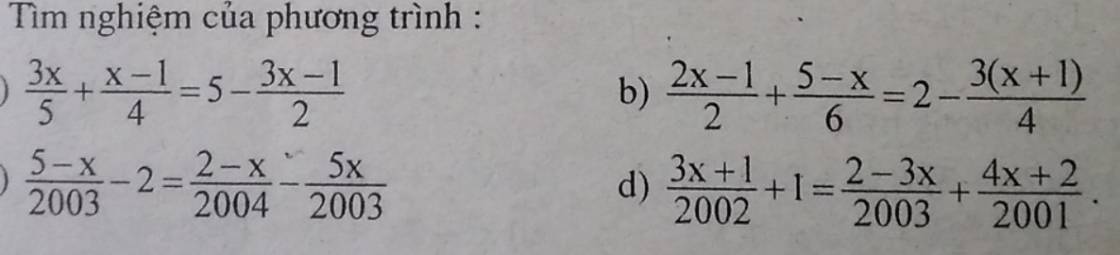

 Giúp vs mn ơi !
Giúp vs mn ơi !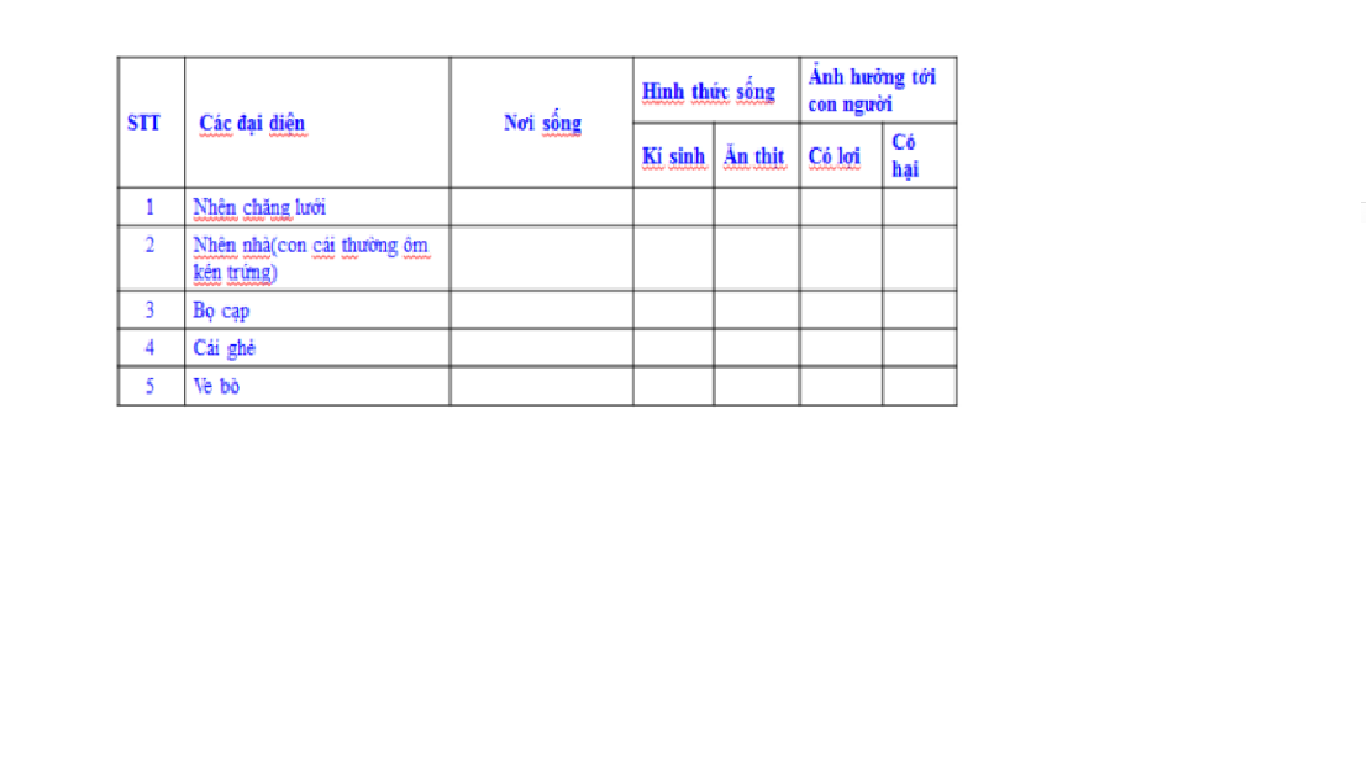
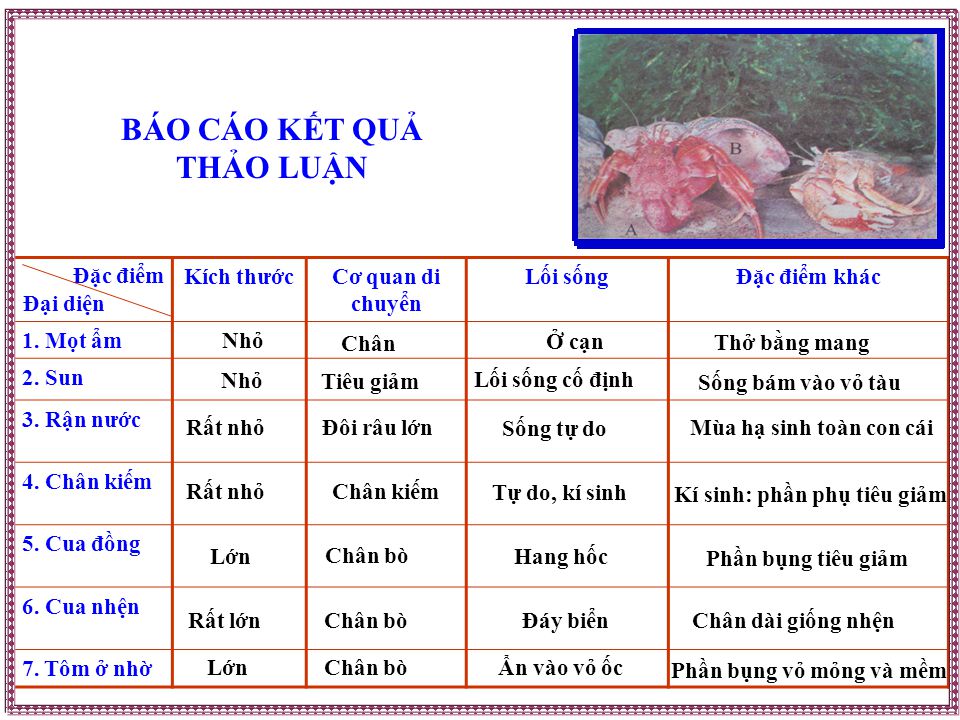

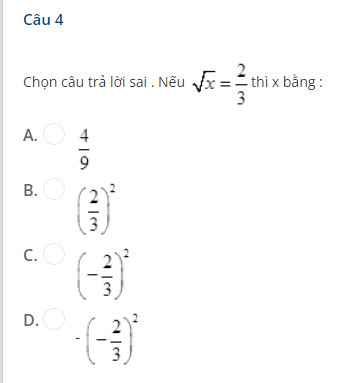 giúp vs mn ơi
giúp vs mn ơi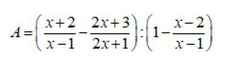 giúp vs mn ơi
giúp vs mn ơi
giả sử AI kéo dài cắt BC tại D.
ta có: \(\frac{BD}{CD}=\frac{c}{b}\Rightarrow BD=\frac{c}{b}CD\Leftrightarrow\overrightarrow{DB}=-\frac{c}{b}\overrightarrow{DC}\Leftrightarrow\overrightarrow{DI}+\overrightarrow{IB}=-\frac{c}{b}\left(\overrightarrow{DI}+\overrightarrow{IC}\right)\Leftrightarrow\left(1+\frac{c}{b}\right)\overrightarrow{DI}=-\overrightarrow{IB}-\frac{c}{b}\overrightarrow{IC}\Leftrightarrow\overrightarrow{ID}=\frac{b}{b+c}\overrightarrow{IB}+\frac{c}{b+c}\overrightarrow{IC}\)
tiếp: Xét tam giác ABD có ID/IA = BD/AB= (ac/b+c)/c=a/b+c
=> ID=(a/b+c)IA
=> \(\overrightarrow{ID}=-\frac{a}{b+c}\overrightarrow{IA}\)
Thế vào (1) ta đc:
\(-\frac{a}{b+c}\overrightarrow{IA}=\frac{b}{b+c}\overrightarrow{IB}+\frac{c}{b+c}\overrightarrow{IC}\)
\(\Leftrightarrow\frac{1}{b+c}\left(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}\right)=0\)
<=> \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=0\): đpcm