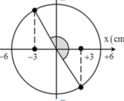
Một vật dao động có x=10cos(2π-π/6).kể từ lúc t=0 đến lúc vật qua li độ 5cm theo chiều dương lần thứ 2013 thì lực hồi phục sinh công dương trong khoảng thời gian nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
28 tháng 1 2019
Chọn C
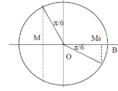
+ Khi t = 0: 
+ Chu kì dao động của vật là T = 1,2s.
+ Lực phục hồi sinh ra công âm khi vật đi từ VTCB ra biên. Trong một chu kì thời gian lực phục hồi sinh công âm trong khoảng nửa chu kì.
+ Vật qua điểm M có li độ -A/2 = 10cm theo chiều âm lần thứ 2013 kể từ lúc t = 0 sau khoảng thời gian là :
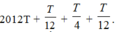
=> Lực phục hồi sinh công âm trong khoảng thời gian:
VT
3 tháng 7 2019
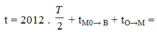
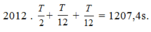
Chọn A.
Lực hồi phục luôn luôn hướng về VTCB, lực hồi phục sinh công dương khi vật chuyển động về VTCB và sinh công âm khi vật chuyển động ra VT biên.
Trong một chu kì, một nửa thời gian (T/2) lực hồi phục sinh công âm một nửa thời gian (T/2) sinh công dương.
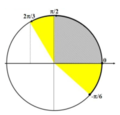
Dừa vào VTLG ta xác định được:
Lần 1, vật qua li độ x = -10 cm theo chiều âm ứng với góc quét từ đến . Trong gia đoạn này khoảng thời gian sinh công dương là T/4 (ứng với phần gạch chéo).
Để đến thời điểm lần thứ 2017, vật qua li độ x = -10 cm theo chiều âm thì cần quét thêm 2016 vòng và thời gian sinh công dương có thêm là 2016.T/2=1008T
Tổng thời gian: T/4 + 1008T = 1209.9 s.
VT
26 tháng 11 2019
Đáp án B
Phương pháp: Sử dụng lí thuyết về lực phục hồi trong dao động điều hòa, dùng đường tròn để tính thời gian
Cách giải:
PT dao động: x = 20cos 5 πt 3 - π 6
Chu kì dao động T = 1,2 s
Ta có hình vẽ sau:
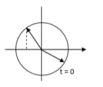
Thời gian vật đi từ thời điểm t = 0 đến khi vật qua li độ x = -10 cm theo chiều âm lần thứ 2017 là:
2016T + 5T/12
Lực phục hồi luôn hướng về VTCB => Lực phục hồi sinh công âm <=> vật chuyển động từ VTCB ra biên
+ trong 2016 chu kì : t1 = 2016.T/2
+ trong 5T/12 còn lại: t2 = T/12 + T/12
=> Thời gian thỏa mãn: Δt = t1 + t2 = 2016.T/2 + T/12 + T/12= 1209,8 s
=> Chọn B
HY
15 tháng 8 2016
\(\Delta l=5cm\)
Vị trí có lực đẩy đàn hồi lần thứ nhất chính là vị trí lò xo bắt đầu bị nén. Tức là qua vị trí -\(x=-\Delta l\).
^
Vị trí ban đầu t = 0 tại M ứng với góc (-90 độ).
Vị trí lực đầy đàn hồi lần thứ nhất tại N x = -5 cm.
=> \(\varphi=\pi+\frac{\pi}{6}=\frac{7\pi}{6}\Rightarrow t=\frac{\varphi}{\omega}=\frac{7\pi}{6.10\pi}=\frac{7}{60}s.\)
20 tháng 6 2019
sai rồi bạn ơi, lực đẩy max là lúc vật ở vị trí -A nhé, denta phi sẽ là 3π/2, và t sẽ là 3/20s
