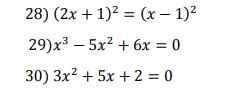🐛` giúp mềnh nha :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


"Lượm" là một trong những bài thơ hay của nhà văn Tố Hữu được đông đảo thế hệ học sinh yêu thích(1).Bài thơ ra đời năm 1949 trong thời kỳ kháng chiến chống thực dân Pháp(2).Bài thơ kể về cuộc đời cách mạng của Lượm(3).Chú bé Lượm hiện lên thật ngây thơ,tinh nghịch,hăng hái(4).Lượm là chú bé liên lạc trên chiến trường đầy nguy hiểm, cạm bẫy luôn rình rập cậu(5).Nhưng vì lòng yêu nước và sự dũng cảm của mình Lượm đã xuất sắc hoàn thành những nhiệm vụ được giao(6).Trong một lần đi giao thư "Thượng khẩn" Lượm đã hy sinh, chú bé ngã xuống ngay trên cánh đồng quê hương và cánh đồng như ôm Lượm vào lòng(7).Tuy Lượm đã hy sinh nhưng hình ảnh của chú còn mãi với quê hương, đất nước và trong lòng mọi người(8).Bằng thể thơ bốn chữ, kết hợp miêu tả và biểu hiện cảm xúc bài thơ đã khắc họa thành công hình ảnh chú bé Lượm(9).Tấm gương dũng cảm và lòng yêu nước của Lượm đáng để mọi người noi theo(10).

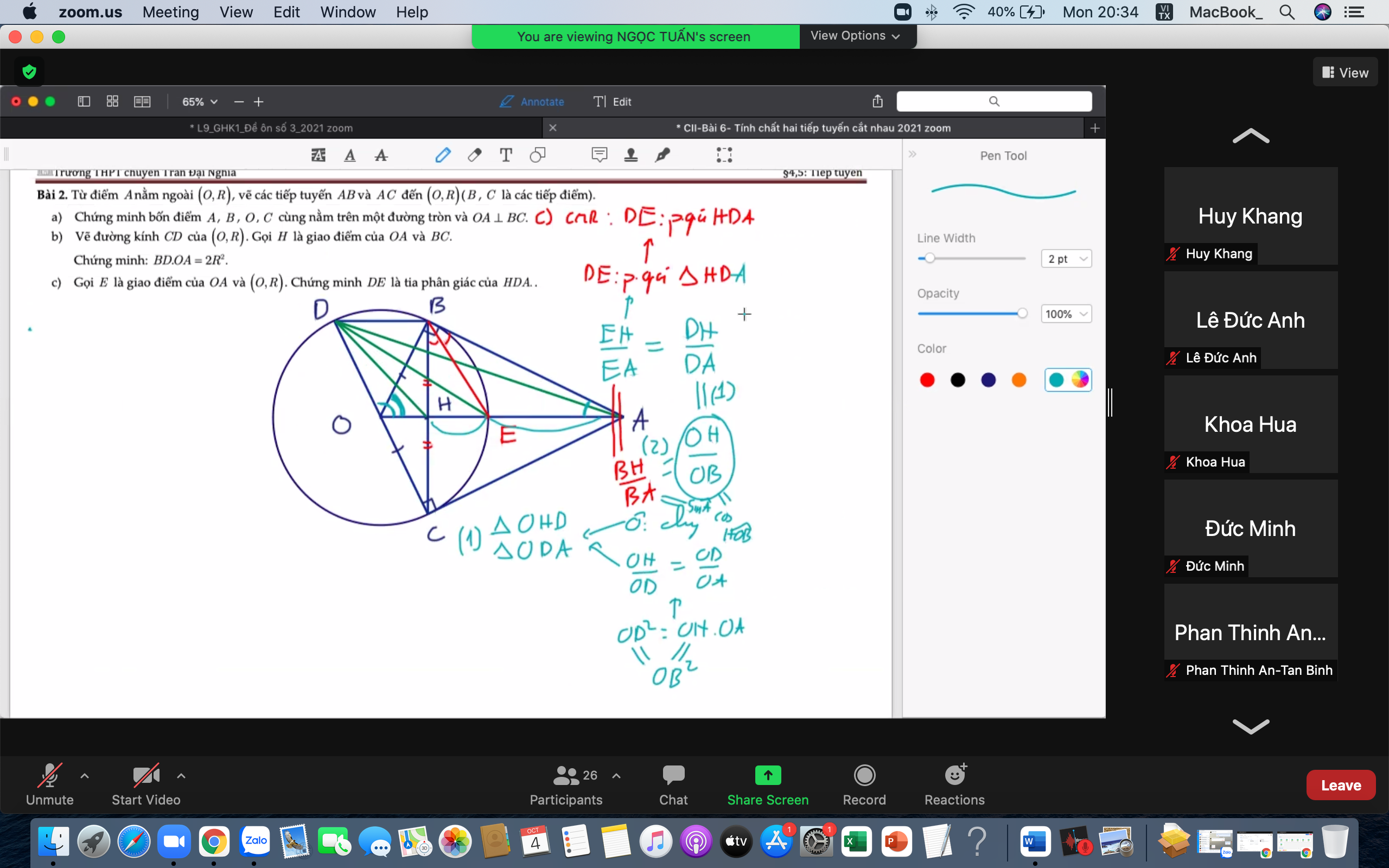
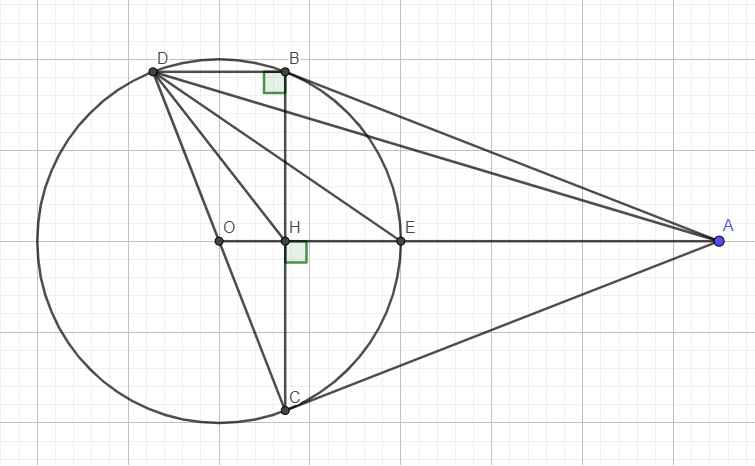
Ta có: \(\widehat{DBC}=90^0\) (nt chắn nửa đường tròn)
\(\Rightarrow BD||OA\) (cùng vuông góc BC)
\(\Rightarrow\widehat{BDE}=\widehat{DEO}\) (slt)
Mà \(\widehat{DEO}=\widehat{ODE}\) (OD=OE=R nên tam giác ODE cân tại O)
\(\Rightarrow\widehat{ODE}=\widehat{BDE}\) (1)
Lại có OH là đường trung bình tam giác BCD (đi qua 2 trung điểm)
\(\Rightarrow BD=2OH\)
Theo câu b: \(BD.OA=2R^2=2OD^2\Rightarrow2OH.OA=2OD^2\)
\(\Rightarrow\dfrac{OH}{OD}=\dfrac{OD}{OA}\)
Hai tam giác ODH và OAD có: \(\left\{{}\begin{matrix}\widehat{O}\text{ chung}\\\dfrac{OH}{OD}=\dfrac{OD}{OA}\end{matrix}\right.\)
\(\Rightarrow\Delta ODH\sim\Delta OAD\Rightarrow\widehat{ODH}=\widehat{OAD}\)
Mà \(\widehat{OAD}=\widehat{BDA}\) (so le trong) (2)
(1);(2) \(\Rightarrow\widehat{HDE}=\widehat{ADE}\) hay DE là phân giác \(\widehat{HDA}\)

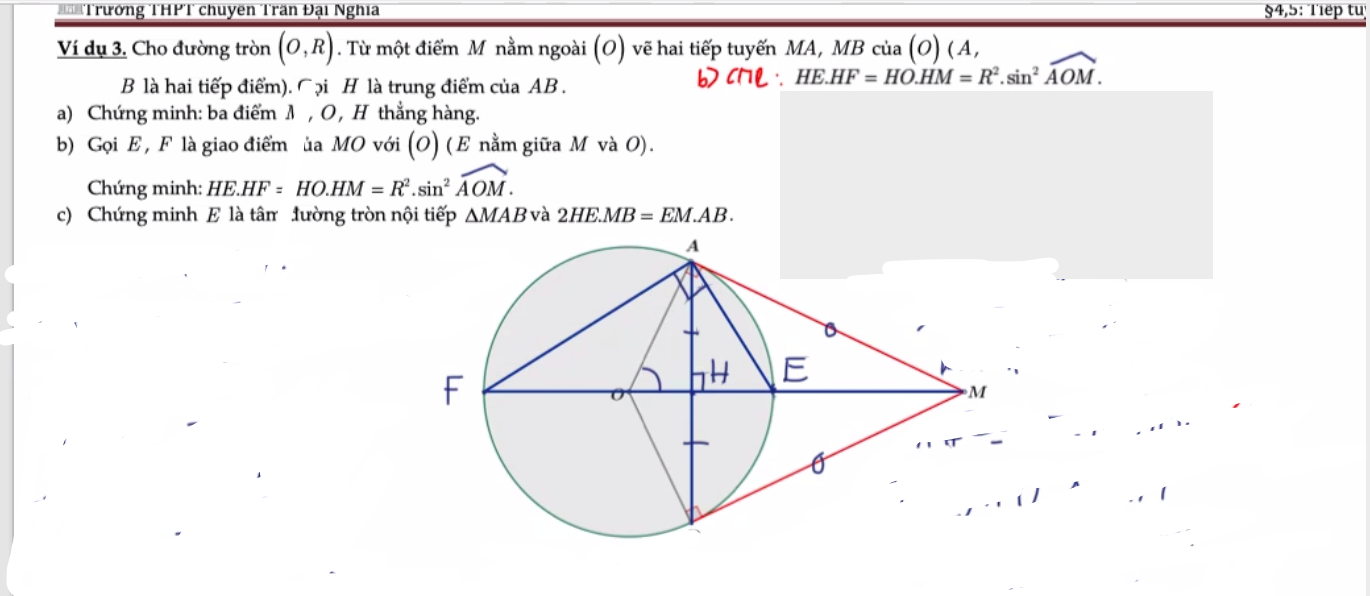
Theo t/c 2 tiếp tuyến \(AM=BM\Rightarrow\Delta ABM\) cân tại M
\(\Rightarrow MH\) là trung tuyến, đường cao, trung trực AB đồng thời là phân giác \(\widehat{AMB}\)
\(\Rightarrow AE=BE\Rightarrow\Delta ABE\) cân tại E
\(\Rightarrow\widehat{ABE}=\widehat{BAE}\)
Mà \(\widehat{ABE}=\widehat{MAE}\) (cùng chắn cung AE)
\(\Rightarrow\widehat{BAE}=\widehat{MAE}\Rightarrow AE\) là phân giác \(\widehat{BAM}\)
\(\Rightarrow\) E là giao điểm 2 đường phân giác trong của tam giác ABM hay E là tâm đường tròn nội tiếp tam giác
Theo định lý phân giác (trong tam giác AHM)
\(\dfrac{HE}{AH}=\dfrac{ME}{AM}\Rightarrow ME.AH=HE.AM\Rightarrow ME.\dfrac{AB}{2}=HE.BM\Rightarrow2HE.BM=ME.AB\)


28.
\(\Leftrightarrow2x+1=x-1\)
\(\Leftrightarrow x=-2\)
29.
\(\Leftrightarrow x^3-2x^2-3x^2+6x=0\)
\(\Leftrightarrow x^2\left(x-2\right)-3x\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x^2-3x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x\left(x-3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\\x=3\end{matrix}\right.\)
30.\(\Leftrightarrow3x^2+3x+2x+2=0\)
\(\Leftrightarrow3x\left(x+1\right)+2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\3x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{2}{3}\end{matrix}\right.\)
\(28,\\ \Leftrightarrow\left[{}\begin{matrix}2x+1=x-1\\2x+1=-x+1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\3x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\\ 29,\\ \Leftrightarrow x\left(x^2-5x+6\right)=0\\ \Leftrightarrow x\left(x^2-2x-3x+6\right)=0\\ \Leftrightarrow x\left[x\left(x-2\right)-3\left(x-2\right)\right]=0\\ \Leftrightarrow x\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=3\end{matrix}\right.\)
\(30,\\ \Leftrightarrow3x^2+3x+2x+2=0\\ \Leftrightarrow3x\left(x+1\right)+2\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x+2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-2}{3}\\x=-1\end{matrix}\right.\)

x(x+y)=2
=> x ; x+y thuộc Ư(2)={-1,-2,1,2}
Ta có bảng :
| x | -1 | -2 | 1 | 2 |
| x+y | -2 | -1 | 2 | 1 |
| y | -1 | 1 | 1 | -2 |
Vậy ta có các cặp x,y thõa mãn (-1,-1);(-2,-1);(1,1);(2,-2)
(x+1)(y-1)=-2
=> x+1 ; y-1 thuộc Ư(-2)={-1,-2,1,2}
Ta có bảng :
| x+1 | -1 | -2 | 1 | 2 |
| y-1 | -2 | -1 | 2 | 1 |
| x | -2 | -3 | 0 | 1 |
| y | -1 | 0 | 3 | 2 |
Vậy ta có các cặp x,y thõa mãn (-2,-1);(-3,0);(0,3);(1,2)
1. x(x+y) = 6
=> x2 + xy = 6(1)
=> x2 và xy là các ước của 6
Ư(6) = {-1;1;-6;6;-3;3;-2;2}
Mà x2 là số chính phương
=> x2= 1
=> x \(\in\){-1;1}
Thay x = 1 vào (1) ta có:
12 + 1.y =6
=> y=6-1
=> y =5
Thay x = -1 vào (1) ta có:
-12 + (-1).y =6
=> (-1).y = 6-1
=> (-1).y = 5
=> y = 5: (-1)
=>y = -5
Vậy x \(\in\){-1;1} ; y\(\in\){5;-5} thỏa mãn yêu cầu đề bài.
2. (x+1) . (y-1) = -2
=> x+1 và y-1 là các ước của -2
Ư(-2) = {-1;1;-2;2}
Ta có bảng sau:
| x+1 | -1 | 2 | -2 | 1 | 1 | 2 |
| y-1 | 2 | -1 | 1 | -2 | 2 | 1 |
| x | 0 | 1 | -3 | 0 | 0 | 1 |
| y | 3 | 0 | 2 | -1 | 3 | 2 |
Vậy các cặp số (x;y) thỏa mãn yêu cầu đề bài là (0;3); (1;0); (-3;2); (0;-1); (0;3); (1;2)