Khối họp ABCD.A'B'C'D' có thể tích =12.Thể tích khối chóp AB'CD' bằng bao nhiu vậy mấy bạn?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C
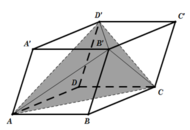
Gọi S là diện tích đáy của tứ giác ABCD và h là chiều cao của khối hộp.
Chia khối hộp ABCD.A'B'C'D' thành khối tứ diện AB'CD' và 4 khối chóp AA'B'D', CB'C'D', B'.BAC, D'.DAC
![]()
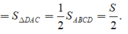
Suy ra
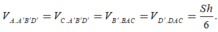
Vậy V A B ' C D '
![]()
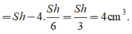

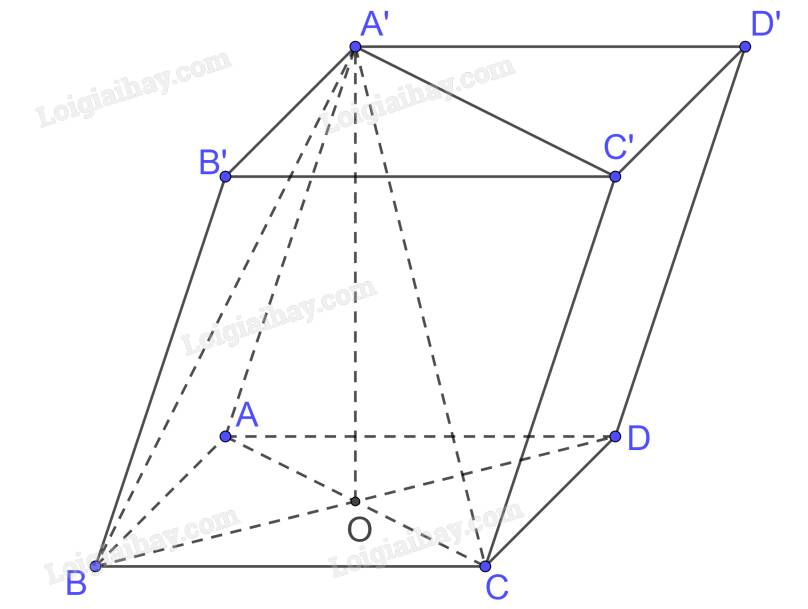
Gọi \(AC \cap BD = \left\{ O \right\}\) mà A’.ABCD là hình chóp đều nên \(A'O \bot \left( {ABCD} \right)\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác A’AO vuông tại O có
\(A'O = \sqrt {A{{A'}^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
\({S_{ABCD}} = {a^2}\)
Vậy khối lăng trụ có thể tích \(V = \frac{1}{3}A'O.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\)
Nếu hình lăng trụ \(ABCD.A'B'C'D'\) xoay lại thành hình lăng trụ AA’D’D.BB’C’C thì thể tích không thay đổi do đó thể tích hình chóp \(A'.BB'C'C\) bằng một phần 3 thể tích hình lăng trụ AA’D’D.BB’C’C vì chung đáy và chung chiều cao kẻ từ A’ xuống đáy BB’C’C.
Thể tích khối chóp là \({V_{A'.BB'C'C}} = \frac{1}{3}.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{{18}}\)

Chọn D
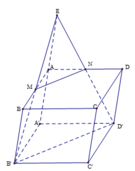
+) Gọi ![]()
Ta có M là trung điểm của AB
=> M là trung điểm EB'
=> N là trung điểm của ED' và AD
+) Ta có 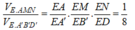
![]()
![]()

Đáp án C

Ta có V A B ' C D ' = V A B C D . A ' B ' C ' D ' − V A B B ' C − V B ' C ' C D ' − V A D C D ' − V A A ' B ' D '
= 12 − 1 6 .4. V A B C D . A ' B ' C ' D ' = 12 − 1 6 .4.12 = 4

Đáp án A
Ta có: V A B C D . A ' B ' C ' D ' = B . h , V O . A ' B ' C ' D ' = 1 3 d O ; A ' B ' C ' D ' . B = 1 3 h . B

Đáp án A
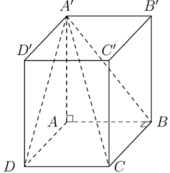
Ta có: hình lập phương ABCD.A'B'C'D' có đường chéo bằng a 3
Suy ra cạnh của hình lập phương bằng a.
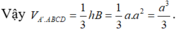 Vậy
V
A
'
.
A
B
C
D
=
1
3
h
B
=
1
3
a
.
a
2
=
a
3
3
Vậy
V
A
'
.
A
B
C
D
=
1
3
h
B
=
1
3
a
.
a
2
=
a
3
3


Bạn xem thí nghiệm trong SGK.
Khi đổ đầy nước vào khối chóp AB'CD' và khối hộp ABCD.A'B'C'D' thì nhận thấy rằng lượng nước trong khối chóp bằng 1/3 lượng nước trong khối hộp, tức \(V_{AB'CD}=\frac{1}{3}.V_{ABCD.A'B'C'D'}=\frac{1}{3}.12=4\)