giải phương trình sau : \(\cos^2x\cos2x=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
0
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
1a.
Đặt \(5x+6=u\)
\(cos2u+4\sqrt{2}sinu-4=0\)
\(\Leftrightarrow1-2sin^2u+4\sqrt{2}sinu-4=0\)
\(\Leftrightarrow2sin^2u-4\sqrt{2}sinu+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinu=\dfrac{3\sqrt{2}}{2}>1\left(loại\right)\\sinu=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow sin\left(5x+6\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+6=\dfrac{\pi}{4}+k2\pi\\5x+6=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{6}{5}+\dfrac{\pi}{20}+\dfrac{k2\pi}{5}\\x=-\dfrac{6}{5}+\dfrac{3\pi}{20}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
1b.
Đặt \(2x+1=u\)
\(cos2u+3sinu=2\)
\(\Leftrightarrow1-2sin^2u+3sinu=2\)
\(\Leftrightarrow2sin^2u-3sinu+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinu=1\\sinu=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(2x+1\right)=1\\sin\left(2x+1\right)=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=\dfrac{\pi}{2}+k2\pi\\2x+1=\dfrac{\pi}{6}+k2\pi\\2x+1=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}+\dfrac{\pi}{4}+k\pi\\x=-\dfrac{1}{2}+\dfrac{\pi}{12}+k\pi\\x=-\dfrac{1}{2}+\dfrac{5\pi}{12}+k\pi\end{matrix}\right.\)
DD
1
7 tháng 5 2016
\(\Leftrightarrow2^{\cos2x-1}\left(2\cos x-1\right)=2\cos^2x\left(2\cos x-1\right)\)
\(\Leftrightarrow\left(2\cos x-1\right)\left(2^{\cos2x}-2\cos^2x\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}\cos x=\frac{1}{2}\\2^{\cos2x}=\cos2x+1\end{array}\right.\)
* Với \(\cos x=\frac{1}{2}\) ta có \(x=\frac{\pi}{3}=k2\pi,k\in Z\)
* Với \(2^{\cos2x}=\cos2x+1\) (*), đặt \(t=\cos2x;t\in\left[-1;1\right]\)
Phương trình trở thành \(2^t-t-1=0\)
Xét hàm số \(f\left(t\right)=2^t-t-1,t\in\left[-1;1\right]\)
Có \(f'\left(t\right)=2^t\ln2-1,t\in\left[-1;1\right];f'\left(t\right)=0\) có đúng 1 nghiệm nên phương trình \(f\left(t\right)=0\) có tối đa 2 nghiệm. Mà \(f\left(0\right)=f\left(1\right)=0\) nên \(t=0;t=1\) là tất cả các nghiệm của phương trình \(f\left(t\right)=0\)
Do đó phương trình (*) \(\Leftrightarrow\left[\begin{array}{nghiempt}\cos2x=0\\\cos2x=1\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=\frac{\pi}{4}+k\frac{\pi}{2}\\x=k\pi\end{array}\right.\) \(k\in Z\)
Vậy phương trình đã cho có 3 nghiệm là :
\(x=\frac{\pi}{3}+k2\pi;x=\frac{\pi}{4}+k\frac{\pi}{2};x=k\pi;k\in Z\)
MM
2
HP
28 tháng 9 2021
a, \(cos2x+4cosx+1=0\)
\(\Leftrightarrow2cos^2x+4cosx=0\)
\(\Leftrightarrow2cosx\left(cosx+2\right)=0\)
\(\Leftrightarrow cosx=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
HP
12 tháng 7 2021
1.
\(2cos4x-3=0\)
\(\Leftrightarrow cos4x=\dfrac{3}{2}\)
Mà \(cos4x\in\left[-1;1\right]\)
\(\Rightarrow\) phương trình vô nghiệm.
2.
\(cos5x+2=0\)
\(\Leftrightarrow cos5x=-2\)
Mà \(cos5x\in\left[-1;1\right]\)
\(\Rightarrow\) phương trình vô nghiệm.
HP
12 tháng 7 2021
3.
\(cos2x+0,7=0\)
\(\Leftrightarrow cos2x=-\dfrac{7}{10}\)
\(\Leftrightarrow2x=\pm arccos\left(-\dfrac{7}{10}\right)+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{arccos\left(-\dfrac{7}{10}\right)}{2}+k\pi\)
4.
\(cos^22x-\dfrac{1}{4}=0\)
\(\Leftrightarrow cos^22x=\dfrac{1}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-\dfrac{1}{2}\\cos2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\pm\dfrac{2\pi}{3}+k2\pi\\2x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k\pi\\x=\pm\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
NJ
0
MA
1
AH
Akai Haruma
Giáo viên
11 tháng 9 2021
Lời giải:
$\tan (\frac{\pi}{2}+x)-3\tan ^2x=\frac{\cos 2x-1}{\cos ^2x}=\frac{2\cos ^2x-2}{\cos ^2x}=\frac{2(\cos ^2x-1)}{\cos ^2x}$
$=\frac{-2\sin ^2x}{\cos ^2x}=-2\tan ^2x$
$\Leftrightarrow \tan (x+\frac{\pi}{2})=\tan ^2x$
Dễ thấy $\tan x=0$ không thỏa mãn nên $\tan x\neq 0$. Do đó pt $\Leftrightarrow \tan ^2x=\tan [\pi +(x-\frac{\pi}{2})]=\tan (x-\frac{\pi}{2})=-\tan (\frac{\pi}{2}-x)=-\cot x =\frac{-1}{\tan x}$
$\Rightarrow \tan ^3x=-1$
$\Rightarrow \tan x=-1$
$\Rightarrow x=\frac{-\pi}{4}+k\pi$ với $k$ nguyên.
CM
14 tháng 3 2017
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
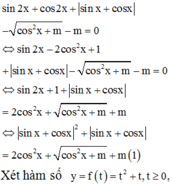
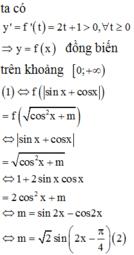
Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
cos2x.cos2x=0
<=>\(\left[\begin{array}{nghiempt}cos^2x=0\\cos2x=0\end{array}\right.\)<=>\(\left[\begin{array}{nghiempt}x=+-\frac{pi}{2}+kpi\\2x=\frac{pi}{2}+kpi\end{array}\right.\),
<=>\(\left[\begin{array}{nghiempt}x=+-\frac{pi}{2}+kpi\\x=\frac{pi}{4}+\frac{kpi}{2}\end{array}\right.\)