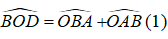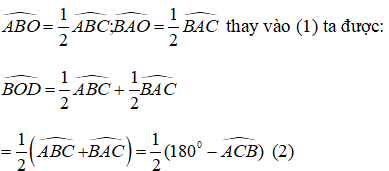3 phân giác trong AD , BE , CF của \(\Delta ABC\) cắt nhau ở O ( AB < AC ). Kẻ OG_|_ BC
a) Tính góc OAC + góc OCA + góc OBC
b) Tính góc BOG - góc COD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ML
21 tháng 4 2016
Vẽ hình ra nhé. Mà ^ kí hiệu là góc ha .
Trong tam giác OGC có góc GOC = 90độ trừ ^OCG
hay ^GOC = 90 độ - ^ACB /2 (1)
^BOD là góc ngoài tam giác AOB tại O => ^BOD = ^BAO+^ABO hay ^BOD= ^BAC/2+^ABC/2
=> ^BOD= (180độ - ^ACB) /2 = 90 độ - ^ ACB/2 (2)
Từ (1) và (2) ta có ^GOC=^BOD
Mà ^BOG+ ^GOD = ^BOD
^COD+^DOG =^COG
=> BOG = COD
21 tháng 4 2016
đÂY LÀ HÌNH Cho tam giác ABC. Vẽ ba đường phân giác AD; BE; CF cắt nhau tại O. Kẻ OG vuông góc BC tại G. Chứng minh rằng góc BOG = góc COD.Mình được gợi ý là dùng góc ngoài. Mình cần cách giải gấp trong một tuần. Giúp mình nhé
CM
24 tháng 4 2018
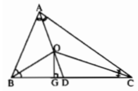
Để chứng minh ∠(BOG) = ∠(COD), ta chứng minh ∠(BOD) = ∠(GOC).
+) Tổng ba góc trong 1 tam giác bằng 180º nên :
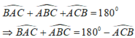
+) Xét tam giác OAB, ta có góc ∠BOD là góc ngoài tam giác tại đỉnh O nên:
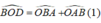
Lại có: BO và AO là tia phân giác của góc B và góc A nên:
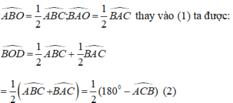
Xét tam giác vuông OCG ta có:
PN
11 tháng 5 2020
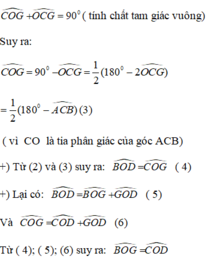
1,
Bài này kinh khủng quá xD chịu r
2,
a, Kẻ AO là pg của EAF^
Do O là trực tâm
Xét tg vuông OEA và tg vuông OFA có :
A1^ = A2^ ( dựng hình )
AO chung
=> tg OEA = tg OFA ( ch-gn )
=> OE = OF ( cạnh tương ứng )
b, Áp dụng định lí pi ta go cho tg ABC vuông tại A có :
BC^2 = 3^2 + 4^2 = 9 + 16 = 25 = 5^2
<=> BC = 5
Thay vào đề ta có :
AB + AC - BC = 2 AE ( Bất đẳng thứ tam giác và đã thỏa mãn )
<=> 4 + 3 - 5 = 2 AE
<=> 2 = 2 AE
<=> AE = 1
27 tháng 7 2015
a) Cho đường thẳng e là đường thẳng vuông góc với Ox qua A
Cho đường thẳng d là đường thẳng vuông góc với Oy qua B
Ta có: Đường thẳng e cắt đường thẳng d tại C mà e _l_ Ox và d _l_ Oy nên góc C= 90 độ
Vậy góc ACB= 90 độ
b) Cho tia phân giác của góc OAC là Az
Vì e_l_Ox tại A và cắt đường thẳng d tại C nên góc OAC=90 độ
Vì Az là tia phân giác của góc OAC nên
góc ADC=góc OAD=\(\frac{gócOAC}{2}\)=\(\frac{90}{2}=45độ\)(1)
c) Cho tia phân giác của góc OBC là Bt
Vì d_l_Oy tại B và cắt đường thẳng e tại A nên góc OBC =90 độ
Vì Bt là tia phân giác của góc OBC nên
góc OEB=góc EBC=\(\frac{gócOBC}{2}=\frac{90}{2}=45độ\) (2)
Ta có góc OEB=góc OAD(=45 độ), dựa vào (1) và (2) mà góc OEB và góc OAD đang ở vị trí đồng vị (3)
Từ (1), (2) và (3) Suy ra AD // BE
18 tháng 5 2022
Tham khảo:
(vì góc BOD là góc ngoài)
(Do BO,CO là các tia phân giác của tam giác ABC)
