Xét quan hệ giữa hai góc vuông trong mỗi biểu thức rồi tính:
a) \(\frac{sin32^o}{cos58^0}\)
b) tg76\(^o\) - cotg14\(^o\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\dfrac{\sin32^0}{\cos58^0}=\dfrac{\sin32^0}{\sin32^0}=1\)
b: \(\tan76^0-\cot14^0=\tan76^0-\tan76^0=0\)

Ta có: 32 ° + 58 ° = 90 °
Suy ra: sin 32 ° = cos 58 ° . Vậy sin 32 ° c o s 58 ° = 1

\(\sin^215^0+\sin^235^0+\sin^255^0+\sin^275^0\)
=1+1
=2

Ta có: 76 ° + 14 ° = 90 °
Suy ra: tg 76 ° = cotg 14 ° . Vậy tg 76 ° – cotg 14 ° = 0

a) Khi \(\alpha = {90^o}\), điểm M trùng với điểm C. (Vì \(\widehat {xOC} = \widehat {AOC} = {90^o}\))
Khi \(\alpha < {90^o}\), điểm M thuộc vào cung AC (bên phải trục tung)
Khi \(\alpha > {90^o}\), điểm M thuộc vào cung BC (bên trái trục tung)
b) Khi \({0^o} < \alpha < {90^o}\) , ta có:
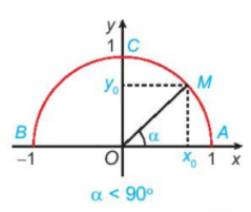
\(\begin{array}{l}\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\)
Vì \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nên \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nên \({y_0} > 0\)
Vậy \(\cos \alpha \) là hoành độ \({x_0}\)của điểm M, \(\sin \alpha \) là tung độ \({y_0}\) của điểm M.
a: \(32^0+58^0=90^0\)
nên \(\sin32^0=\cos58^0\)
\(\Leftrightarrow\dfrac{\sin32^0}{\cos58^0}=1\)
b: \(76^0+14^0=90^0\)
nên \(\tan76^0=\cot14^0\)
\(\Leftrightarrow\tan76^0-\cot14^0=0\)