cho hình thanh ABCD (AB//CD),(CD,AD=AB)
a, chứng minh góc ADB = góc BDC
b,CA có phải là phân giác của góc O không vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GH
22 tháng 6 2023
2)
Có: \(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\AD=BC\left(2.cạnh.bên.hình.thang.cân\right)\end{matrix}\right.\)
\(\Rightarrow AB=BC\Rightarrow\Delta ABC.cân.tại.B\)
Mà AB // ED (gt)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
=> CA là tia phân giác của góc C.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 7 2023
Bài 5
\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)
\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)
\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)
\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)
Xét tg ADE có
\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)
\(\Rightarrow Ax\perp Dy\)
Bài 6:
a/
Ta có
AB//CD => AB//DE
BE//AB (gt)
=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)
b/
CD - DE = CE
Mà AB = DE (cmt)
=> CD - AB = CE
c/
Xét tg BCE có
BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)
Mà CE = CD - DE và DE = AB (cmt) và BE = AD
=> BC+BE = BC + AD>CE = CD - AB
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
20 tháng 7 2023
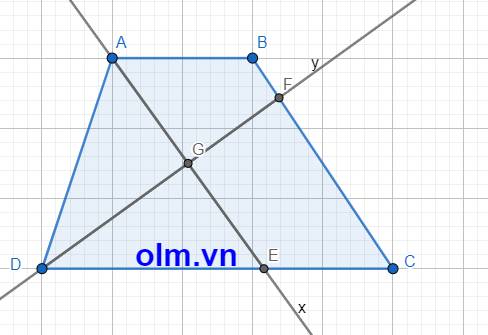
Gọi G là giao điểm của hai đường phân giác Ax và By
Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)
\(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\))
\(\widehat{ADE}\) + \(\widehat{DAB}\) = 1800 (vì hai góc là hai góc trong cùng phía)
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 1800 = 900
Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 1800 (tổng ba góc trong 1 tam giác bằng 1800)
⇒ \(\widehat{DGA}\) = 1800 - 900 = 900
Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)
14 tháng 10 2021
Ta có: OA = OC (gt)
⇒ ∆ OAC cân tại O
⇒ˆA1=1800–ˆAOC2⇒A^1=1800–AOC^2 (tính chất tam giác cân) (1)
OB = OD (gt)
⇒ ∆ OBD cân tại O
⇒ˆB1=1800–ˆBOD2⇒B^1=1800–BOD^2 (tính chất tam giác cân) (2)
ˆAOC=ˆBODAOC^=BOD^ (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra: ˆA1=ˆB1A^1=B^1
⇒ AC // BD (vì có cặp góc ở vị trí so le trong bằng nhau)
Suy ra: Tứ giác ACBD là hình thang
Ta có: AB = OA + OB
CD = OC + OD
Mà OA = OC, OB = OD
Suy ra: AB = CD
Vậy hình thang ACBD là hình thang cân.
M
22 tháng 9 2016
cho mình xin lỗi ,câu c mình ghi sai 1 câu nhưng ko quan trọng lắm
"hình bình hành có 2 cạnh kề bằng nhau là hình thoi,bạn xem lại nhan,do mình bấm vội nhưng giải đúng đó
M
22 tháng 9 2016
bạn ghi đề sai rồi ,phải là AB=BC=AD và CD=2AB nhan
hình bạn tự vẽ đi nhan
câu a:ta có AB//CD(vì ABCD là hình thang) nên góc BDC=góc ABD(1)
lại có AD=AB(gt)nên tamgiacs ADB cân tại A nên góc ABD=góc ADB(2)
từ (1) và (2) ta có góc ADB =góc BDC nên BD là phân giác goc ADC
câu b:xét tam giác ADC và tam giác BDC ,có
AD=BC(gt);DC :chung và góc D=góc C(vì ABCD là hình thang cân) nên 2 tam giác này bằng nhau nên AC=BD
câu c:gọi K là trung điểm CD ,ta có AB=1/2 CD =CK,mà AB=BC(gt)nên BC=CK(3)
lại có AB=1/2CD=DK mà AB//DK(vì ABCD là hình thang) nên ABKD là hình bình hành
mặt khác AB=AD(gt) nên ABKD là hình thoi(vì hình bình nhành có 2 cạnh bên bằng nhau là hình thoi đó)
=>BK=AB mà BC=AB =>BK=BC(4)
từ (3)và (4)=>BK=BC=CK nên BCK là tam giác đều nên góc C=60 độ và bằng góc D,=> góc A=120độ và bằng góc B
XONG,MỎI TAY QUÁ BN K CHO MÌNH NHAN,BYE
Có: AB // CD
=> góc ABD = góc BDC (so le trong)
=> AD // BC (dấu hiệu nhận biết 2 đường thẳng //)
=> Hình thang ABCD là hình bình hành
Mà: AB = AD = CD
=> Hình bình hành ABCD là hình thoi
=> Góc ADB = góc BDC (t/chất của hình thoi)
b) Câu này nếu đề là "CA có phải là p/giác của góc C (hoặc góc A) ko vì sao?" thì đáp án là:
- Vì CA là đường chéo của hinh thoi ABCD nên suy ra CA là đường p/giác của góc C (hoặc góc A) (t/chất của hình thoi)