Gọi vecto GA + GB+GC =veto 0. CMR G là trọng tâm tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 9
\(\overrightarrow{GA}+\overrightarrow{GB}-\overrightarrow{GC}\)
\(=\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{CG}\)
\(=\overrightarrow{GA}+\overrightarrow{CB}\)
Qua C, lấy K sao cho \(\overrightarrow{CK}=\overrightarrow{GA}\)
=>CK//GA và CK=GA
Xét ΔABC đều có G là trọng tâm
nên AG⊥BC
=>CK⊥CB
Xét ΔABC đều có G là trọng tâm
nên G là tâm đường tròn ngoại tiếp ΔABC
=>GA=GB=GC
Xét (G) có \(\hat{BAC}\) là góc nội tiếp chắn cung BC
nên \(\hat{BGC}=2\cdot\hat{BAC}=120^0\)
Xét tứ giác AGCK có
AG//CK
AG=CK
Do đó: AGCK là hình bình hành
Hình bình hành AGCK có AG=GC
nên AGCK là hình thoi
=>CA là phân giác của góc GCK
=>\(\hat{GCK}=2\cdot\hat{GCA}=60^0\)
Xét ΔGCK có GC=KC và \(\hat{GCK}=60^0\)
nên ΔGCK đều
=>\(\hat{KGC}=60^0\)
\(\hat{BGC}+\hat{KGC}=120^0+60^0=180^0\)
=>B,G,K thẳng hàng
Trên tia đối của tia GC, lấy E sao cho GC=GE
=>G là trung điểm của EC
Ta có: EC=2GC
BK=2GB
mà GC=GB
nên EC=BK
Xét tứ giác BCKE có
G là trung điểm chung của BK và CE
=>BCKE là hình bình hành
Hình bình hành BCKE có \(\hat{BCK}=90^0\)
nên BCKE là hình chữ nhật
=>\(\overrightarrow{CB}+\overrightarrow{CK}=\overrightarrow{CE}=2\cdot\overrightarrow{CG}\)
\(\overrightarrow{GA}+\overrightarrow{CB}=\overrightarrow{CK}+\overrightarrow{CB}=2\cdot\overrightarrow{CG}\)
=>\(\overrightarrow{GA}+\overrightarrow{GB}-\overrightarrow{GC}=2\cdot\overrightarrow{CG}\)
6 tháng 10 2020
mk bận đi ch nên chỉ tạm câu a nha
vẽ 3 đường trung tuyến AD ; BE ; CF
VT =
\(GA+GB+GC\) ( nhớ thêm dấu vec tơ nha )
\(=-\frac{2}{3}AD-\frac{2}{3}BE-\frac{2}{3}CF\)
\(=-\frac{2}{3}\cdot\frac{1}{2}\left(AB+BC\right)-\frac{2}{3}\cdot\frac{1}{2}\left(BA+BC\right)-\frac{2}{3}\cdot\frac{1}{2}\left(CA+CB\right)\) ( quy tắc hình bình hành )
\(=-\frac{1}{3}\left(AB+AC\right)-\frac{1}{3}\left(BA+BC\right)-\frac{1}{3}\left(CA+CB\right)\)
\(=-\frac{1}{3}AB-\frac{1}{3}AC-\frac{1}{3}BA-\frac{1}{3}BC-\frac{1}{3}CA-\frac{1}{3}CB\)
\(=0=VP\)
22 tháng 10 2023
a: Gọi M là trung điểm của AB
Xét ΔABC có
G là trọng tâm
M là trung điểm của AB
Do đó: CG=2/3CM
=>CG=2GM
=>\(\overrightarrow{CG}=2\overrightarrow{GM}\)
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\)
\(=2\overrightarrow{GM}+\overrightarrow{GC}\)
\(=\overrightarrow{CG}+\overrightarrow{GC}=\overrightarrow{0}\)
b: \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
\(=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\)
\(=3\cdot\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(=3\cdot\overrightarrow{MG}\)
)
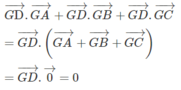
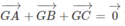* cái này là công thức rồi bn o cần chứng minh đâu
công thức : cho tam giác ABC ; nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
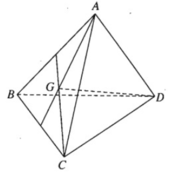
Gọi M trung điểm BC
G đối xứng D qua M
=> tứ giác BGCD là hình bình hành
=> GD=2.GM (Hình bình hành có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mà AG = 2.GM ( \(\dfrac{AG}{GM}=\dfrac{2}{1},GA=\dfrac{2}{3}AM\) )
⇒ AG=GD
Mặt khác, G ϵ AD
⇒\(\overrightarrow{AG}=\overrightarrow{GD}\)
Ta có \(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GD}\) (Quy tắc hình bình hành)
Nên \(\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GA}\) = \(\overrightarrow{GD}+\overrightarrow{GA}\)
Mà \(\overrightarrow{AG}=\overrightarrow{GD}\) (cmt)
⇒\(\overrightarrow{AG}+\overrightarrow{GA}=\overrightarrow{AG}-\overrightarrow{AG}=\overrightarrow{O}\)