Tìm x, biết 5x +5x+1 +5x+2 <10...00 (18 số 0)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PC
0
PL
2
14 tháng 7 2023
a: =>2^4x<2^28
=>4x<28
=>x<7
b: =>5^3x+3<5
=>3x+3<1
=>3x<-2
=>x<-2/3
11 tháng 2 2022
KHÓOOOOOOOOOO QUÁAAAAAAA ĐIIIIIIIIIIIIIIIIIIII CHẾTTTTTTTTTTTTT
9 tháng 8 2021
Bạn thử xem lại đề nhé, giữa 3 số này là dấu cộng hay dấu nhân.
Nếu là dấu cộng thì ta có:
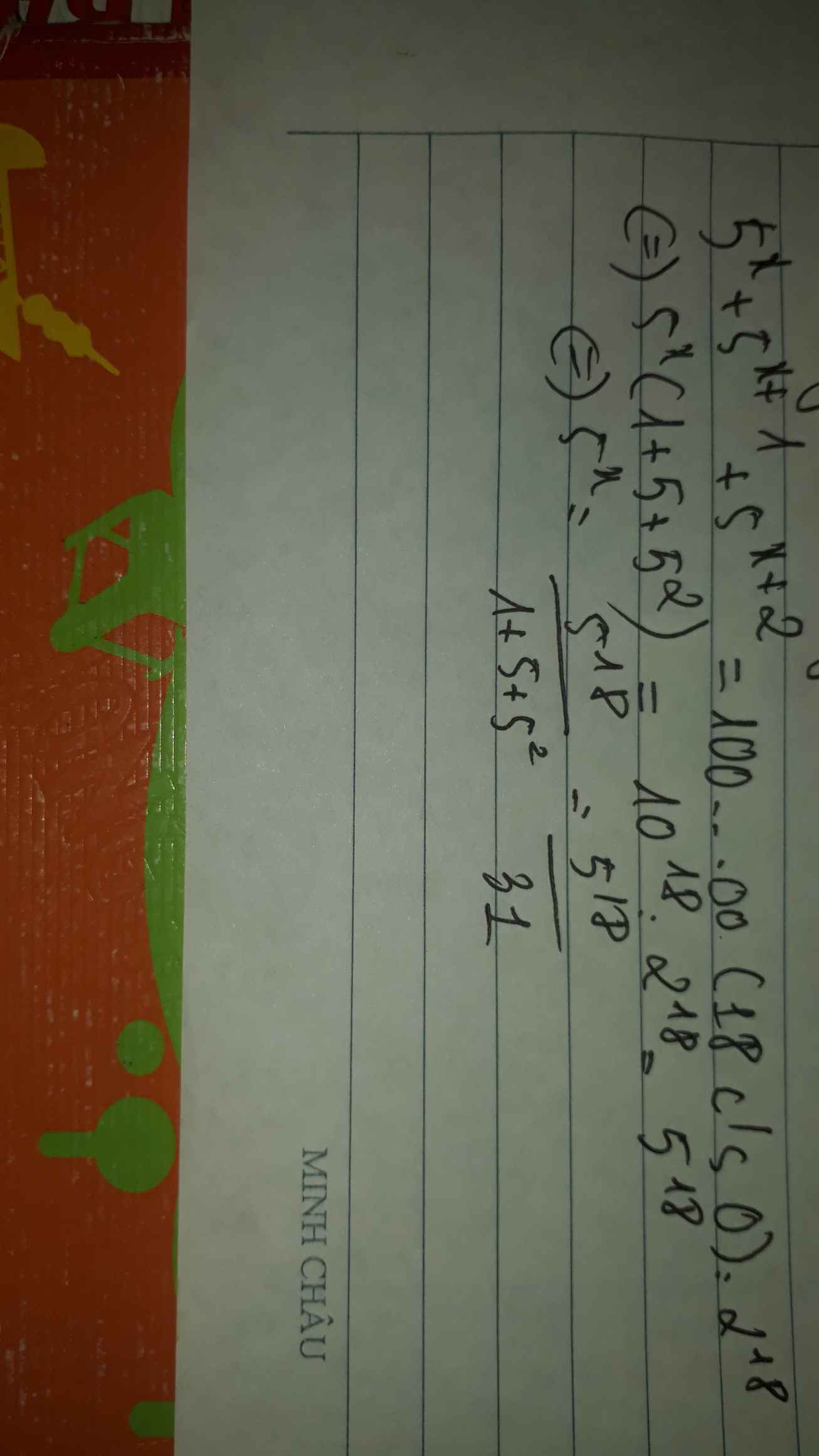
Nếu là dấu nhân thì ta có:
KT
0
H
1
11 tháng 9 2021
\(5x\left(3x^2y-2xy^2+1\right)-3xy\left(5x^2-3xy\right)+x^2y^2-10=0\)
\(\Leftrightarrow15x^3y-10x^2y^2+5x-15x^3y+9x^2y^2+x^2y^2-10=0\)
\(\Leftrightarrow5x=10\Leftrightarrow x=2\)
MC
2
H9
HT.Phong (9A5)
CTVHS
22 tháng 9 2023
\(\dfrac{5x-10}{77x^2+1}=0\)
Mà: \(77x^2+1\ge1>0\forall x\)
\(\Rightarrow5x-10=0\)
\(\Rightarrow5x=10\)
\(\Rightarrow x=\dfrac{10}{5}\)
\(\Rightarrow x=2\)
22 tháng 9 2023
\(\left(5x-10\right):\left(77x^2+1\right)=0\)
\(TH1:5x-10=0\)
\(\Rightarrow5x=10\)
\(\Rightarrow x=10:5\)
\(\Rightarrow x=2\)
\(TH2:77x^2+1=0\)
\(\Rightarrow77x^2=-1\) \(\left(vô.lý\right)\)
\(\Rightarrow\left(-1\ne0\right)\)
Vậy nghiệm của đa thức \(\left(5x-10\right):\left(77x^2+1\right)=0\) là: \(x=2\)
TD
1
Lời giải:
$5^x+5^{x+1}+5^{x+2}<10^{18}$
$5^x(1+5+5^2)< 10^{18}$
$5^x.31< 10^{18}$
$5^x< \frac{10^{18}}{31}$
Về mặt tính toán thì bài toán này không phù hợp lắm. Bạn xem lại nhé.