Hai nguồn sóng kết hợp S1 và S2 trên mặt chất lỏng cách nhau a = 30 cm, dao động điều hòa cùng pha, phát ra hai sóng có cùng bước sóng 10 cm. Xét điểm A trên mặt chất lỏng nằm trên đường thẳng vuông góc với S1S2 tại S3 và cách S1 một khoảng d. Giá trị cực đại của d để tại A là cực đại giao thoa là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Cách 1: vẽ hình ra: ta thấy ngay: để tại A là cực đại giao thoa, đồng thời đoạn d lớn nhất
thì A chính là giao của hypebol vân cực đại thứ nhất với đường thẳng vuông góc
S
1
S
2
q
u
a
S
1
Khi đó, ta có:
A
S
2
-
A
S
1
=
1
×
λ
⇔
d
2
+
4
-
d
=
1
⇒
d
=
1
,
5
m
Cách 2: dùng kiến thức hypebol
lập pt hệ trục tọa độ Oxy với O là trung điểm của
S
1
S
2
khi đó, điểm A thuộc đường thẳng x = 1 và đồng thời thuộc hypebol vân cực đại thứ nhất.
pt hybpebol:
x
2
a
2
-
y
2
b
2
=
1
Trong đó:
a
=
λ
2
=
0
,
5
;
b
2
=
c
2
-
a
2
=
O
S
1
2
-
a
2
=
1
2
-
0
,
5
2
=
0
,
75
;
x
=
1
;
y
=
d
Như vậy, tính được ngay: d = 1,5 m.

Đáp án A
Bước sóng: 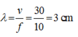
Số vân cực đại và cực tiểu thỏa mãn:
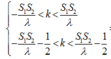
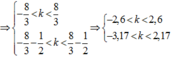
Như vậy có 5 vân cực đại và 6 vân cực tiểu.

Đáp án B
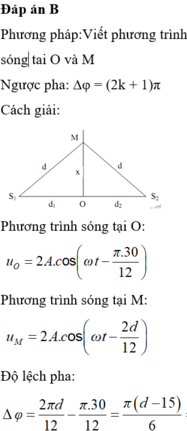
Phương pháp:Viết phương trình sóng tai O và M
Ngược pha: ∆φ = (2k + 1)π
Cách giải:
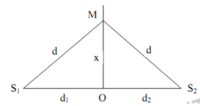



Đáp án: D
HD Giải: Độ lệch pha của hai sóng kết hợp
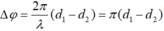
![]()
=> ![]()
=> ![]()
<=> ![]()
=> ![]()
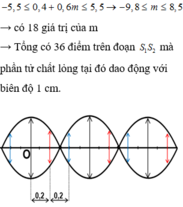
Trên đường nối S1S2 số điểm dao động với biên độ 13 cm thỏa mãn:
-AB < d1 - d2 < AB
=> -10,5 < k < 9,5
Suy ra có 20 điểm

chọn đáp án B
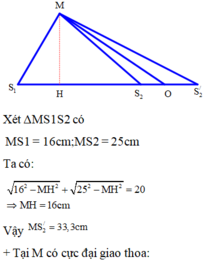
số điểm dao động với biên độ cực đại trên S 1 S 2 thoả mãn
-
S
1
S
2
λ
≤
k
≤
-
S
1
S
2
λ
⇒
-
5
,
5
≤
k
≤
5
,
5
A thuộc đường vuông góc với
S
1
S
2
qua
S
1
,để A gần
S
1
nhất dao động với biên độ cực đại thì A thuộc vân cực đại bậc -5
ta có
A
S
1
-
A
S
2
=
-
5
λ
A
S
1
2
+
S
1
S
2
2
=
A
S
2
2
L
2
+
S
1
S
2
2
=
(
L
+
2
)
2
⇒
L
=
0
.
21
m