Bài 1 Tính giá trị biểu thức
1, COS 330-Sin 570+Sin2 440+Sin2460
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HB
0
NT
1
15 tháng 10 2023
\(B=cos^2x+sin^2x+tan^2x\)
\(=1+tan^2x\)
\(=\dfrac{1}{cos^2x}=1:\dfrac{1}{4}=4\)
HP
6 tháng 8 2021
\(M=sinx.cosx+\dfrac{sin^2x}{1+cotx}+\dfrac{cos^2x}{1+tanx}\)
\(=sinx.cosx+\dfrac{sin^2x}{\dfrac{cosx+sinx}{sinx}}+\dfrac{cos^2x}{\dfrac{cosx+sinx}{cosx}}\)
\(=sinx.cosx+\dfrac{sin^3x+cos^3x}{cosx+sinx}\)
\(=sinx.cosx+\dfrac{\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{cosx+sinx}\)
\(=sinx.cosx+sin^2x+cos^2x-sinx.cosx\)
\(=sin^2x+cos^2x=1\)
CM
25 tháng 3 2018
Chọn B.
Ta có: 1 + cos2α = 2cos2α và sin2α = 2sinα.cosα.
Mà tanα = 2 nên cot α = 1/2
Suy ra:
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
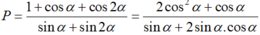
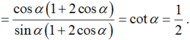
a/\(sina-1=2sin\dfrac{a}{2}.cos\dfrac{a}{2}-sin^2\dfrac{a}{2}-cos^2\dfrac{a}{2}=-\left(sin\dfrac{a}{2}-cos\dfrac{a}{2}\right)^2\)
b/\(P=\dfrac{cosa+cos5a+2cos3a}{sina+sin5a+2sin3a}=\dfrac{2cos3a.cos2a+2cos3a}{2sin3a.cos2a+2sin3a}=\dfrac{2cos3a\left(cos2a+1\right)}{2sin3a\left(cos2a+1\right)}=cot3a\)
c/\(P=sin\left(30+60\right)=sin90=1\)
d/
\(A=cos\dfrac{2\pi}{7}+cos\dfrac{6\pi}{7}+cos\dfrac{4\pi}{7}\Rightarrow A.sin\dfrac{\pi}{7}=sin\dfrac{\pi}{7}.cos\dfrac{2\pi}{7}+sin\dfrac{\pi}{7}cos\dfrac{4\pi}{7}+sin\dfrac{\pi}{7}.cos\dfrac{6\pi}{7}\)
\(=\dfrac{1}{2}sin\dfrac{3\pi}{7}-\dfrac{1}{2}sin\dfrac{\pi}{7}+\dfrac{1}{2}sin\dfrac{5\pi}{7}-\dfrac{1}{2}sin\dfrac{3\pi}{7}+\dfrac{1}{2}sin\dfrac{7\pi}{7}-\dfrac{1}{2}sin\dfrac{5\pi}{7}\)
\(=-\dfrac{1}{2}sin\dfrac{\pi}{7}\Rightarrow A=-\dfrac{1}{2}\)
e/
\(tan\dfrac{\pi}{24}+tan\dfrac{7\pi}{24}=\dfrac{sin\dfrac{\pi}{24}}{cos\dfrac{\pi}{24}}+\dfrac{sin\dfrac{7\pi}{24}}{cos\dfrac{7\pi}{24}}=\dfrac{sin\dfrac{\pi}{24}cos\dfrac{7\pi}{24}+sin\dfrac{7\pi}{24}cos\dfrac{\pi}{24}}{cos\dfrac{\pi}{24}.cos\dfrac{7\pi}{24}}\)
\(=\dfrac{sin\left(\dfrac{\pi}{24}+\dfrac{7\pi}{24}\right)}{\dfrac{1}{2}cos\dfrac{\pi}{4}+\dfrac{1}{2}cos\dfrac{\pi}{3}}=\dfrac{2sin\dfrac{\pi}{3}}{cos\dfrac{\pi}{4}+cos\dfrac{\pi}{3}}=\dfrac{\sqrt{3}}{\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}}=\dfrac{2\sqrt{3}}{\sqrt{2}+1}\)
BC
2
13 tháng 8 2023
Ta có \(2\sin x\cos x=\left(\sin x+\cos x\right)^2-\left(\sin^2x+\cos^2x\right)\)
\(=\left(\dfrac{3}{4}\right)^2-1=-\dfrac{7}{16}\)
Từ đó \(A=\left|\sin x-\cos x\right|\)
\(\Rightarrow A^2=\left(\sin x-\cos x\right)^2\)
\(A^2=\sin^2x+\cos^2x-2\sin x\cos x\)
\(A^2=1+\dfrac{7}{16}=\dfrac{23}{16}\)
\(\Rightarrow A=\dfrac{\sqrt{23}}{4}\) (do \(A\ge0\))
XO
13 tháng 8 2023
Có \(\cos x+\sin x=\dfrac{3}{4}\)
\(\Leftrightarrow\left(\cos x+\sin x\right)^2=\dfrac{9}{16}\)
\(\Leftrightarrow2.\sin x.\cos x+1=\dfrac{9}{16}\)
\(\Leftrightarrow\sin x.\cos x=-\dfrac{7}{32}\)
Lại có \(\left(\cos x+\sin x\right)^2=\left(\cos x-\sin x\right)^2+4.\sin x.\cos x=\dfrac{9}{16}\)
\(\Leftrightarrow\left(\cos x-\sin x\right)^2=\dfrac{23}{16}\)
\(\Leftrightarrow\left|\sin x-\cos x\right|=\dfrac{\sqrt{23}}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2021
\(tana-cota=2\sqrt{3}\Rightarrow\left(tana-cota\right)^2=12\)
\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)
\(\Rightarrow P=4\)
\(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\)
\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)
\(P=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)
giá trị của biểu thức bằng 1