tam giác ABC cân tại A Gọi M N D theo thứ tự là trung điểm AB AC BC
chứng minh AMDN là hình thoi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 7 2018
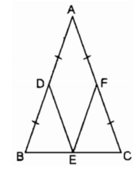
Ta có: E là trung điểm của BC (gt)
D là trung điểm của AB (gt) nên ED là đường trung bình của ∆ ABC
DE = AF = 1/2 AC (1)
F là trung điểm của AC (gt) nên EF là đường trung bình ∆ ABC ⇒ EF = AD = 1/2 AB (2)
AB = AC (gt)
Từ (1), (2) và (gt) suy ra: AD = DE = EF = AF
Vậy tứ giác ADEF là hình thoi.
4 tháng 9 2021
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC và \(NM=\dfrac{BC}{2}\)
mà \(BH=CH=\dfrac{BC}{2}\)
nên NM=BH=CH
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{MBC}=\widehat{NCB}\)
nên BMNC là hình thang cân
Xét tứ giác MNHB có
MN//BH
MN=BH
Do đó: MNHB là hình bình hành
b: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH\(\perp\)BC
Xét tứ giác AHCD có
N là trung điểm của đường chéo AC
N là trung điểm của đường chéo HD
Do đó: AHCD là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
5 tháng 11 2021
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Hình bạn tự vẽ nhé!
Có: `M,N` là trung điểm của `AB,AC`
`=>MN` là đường trung bình của `\DeltaABC`
`=> MN //// BC`
Tương tự: `MD,ND` là đường trung bình của `\DeltaABC`.
`=> MD //// AC ; ND ////AB`
`=> MD //// AN ; ND //// AM`
`=>` Tứ giác `AMDN` là hình bình hành. (1)
Xét `\DeltaABC` cân tại `A` có: `D` là trung điểm của `BC`
`=> AD` vừa là trung tuyến, vừa là đường cao.
`=> AD \bot BC`
Mà `BC////MN`
`=> AD \bot MN`. (2)
Từ (1) và (2) `=> AMDN` là hình thoi.
theo bài ra AB,AC,BC là có các trung điểm thứ tự M,N,D
=>AM=MB,AN=NC,BD=DC
=>MN là đường trung bình tam giác ABC=>MN//BC
=>MD là...................................................=>MD//AC
=>ND là....................................................=>ND//AB
=>AMDN là hình bình hành,
gọi giao điểm MN và AD là K
mà AMDN là hình bình hành nên MN và AD cắt nhau tại trung điểm K mỗi đường (1)
Do tam giác ABC cân có AD là trung tuyến nên đồng thời là đường cao
\(=>AD\perp BC\) mà MN//BC=>\(AD\perp MN\)(2)
từ (1)(2)=>AMDN là hình thoi