9sinx +6cosx - 3sin2x + cos2x = 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(4cos^2x-\left(4cos^3x-3cosx\right)=6cosx+2\left(1+2cos^2x-1\right)\)
\(\Leftrightarrow4cos^3x+3cosx=0\)
\(\Leftrightarrow cosx\left(4cos^2x+3\right)=0\)
\(\Leftrightarrow cosx=0\)
\(\Rightarrow x=\dfrac{\pi}{2}+k\pi\)

Đáp án B
Ta có: P T ⇔ 4 c os 3 x − 3 cos x + 2 sin 2 x + 9 sin x − 5 = 0
⇔ cos x 4 c os 2 x − 3 + 2 sin 2 x + 9 sin x − 5 = 0 ⇔ cos x 1 − 4 sin 2 x + 2 sin x − 1 s inx + 5 = 0 ⇔ 2 sin x − 1 cos x + 2 sin x cos x + s inx + 5 = 0 ⇔ 2 sin x − 1 s inx + cos x + sin 2 x + 5 = 0 ⇔ 2 sin x − 1 = 0 ⇔ s inx = 1 2 ⇔ x = π 6 k 2 π x = 5 π 6 + k 2 π
Với x ∈ 0 ; 3 π ⇒ x = π 6 ; 5 π 6 ; π 6 + 2 π ; 5 π 6 + 2 π ⇒ T = 6 π .


cos 2 x = 3 sin 2 x + 3
Ta thấy cosx = 0 không thỏa mãn phương trình. Với cosx ≠ 0, chia hai vế của phương trình cho cos2x ta được:
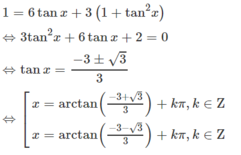
Thấy : \(cos\) \(2x=1-2sin^2\left(x\right)\)
\(sin2x=2sinx.cosx\)
Thay vào ta được :
9 sinx + 6cosx - 6. sinx.cosx +1 -2.sin^2(x) -8 =0
9. (sinx-1) + 6.cosx. (1-sinx) +2 -2.sin^2(x) =0
9.(sinx-1) + 6cosx.(1-sinx) +2. (1-sinx) (1+sinx) =0
* TH1 : sinx=1 -> x =.....
* TH2 : sinx khác 1
Chia cả 2 vế cho sinx-1 ta được :
9 - 6.cosx -2 (1+sinx) =0
<--> 7 -6cosx - 2.sinx = 0
<--> 7- 4.cosx -2. (sinx+cosx)= 0
<-->7 - 4.cosx -2.căn2. sin(x+45) = 0 (1)
ta thấy Vế trái luôn > 0 với mọi x nên (1) vô nghiệm
Kết luận : sinx=1