Cho hình bình hành ABCD. Chứng minh rằng
\(AB^2+BC^2+CD^2+DA^2=AC^2+BD^2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Từ \(2\overrightarrow{ỊJ}=\overrightarrow{AB}+\overrightarrow{CD}\) suy ra
\(AB^2+BC^2+CD^2+DA^2=AC^2+BD^2+4IJ^2\Leftrightarrow CB^2+DA^2=CA^2+DB^2+2AB^2.CD^2\)
\(\Leftrightarrow2.\overrightarrow{AB}\overrightarrow{CD}=AD^2-AC^2+BC^2-BD^2\)

a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình
=>EF//AC và EF=AC/2(1)
Xét ΔCDA có
G là trung điểm của CD
H là trung điểm của DA
Do đó: GH là đường trung bình
=>GH//AC và GH=AC/2(2)
Từ (1) và (2) suy ra EF//GH và EF=GH
hay EFGH là hình bình hành
b: EF=GH=AC/2=3(cm)
FG=EH=BD/2=4(cm)

Tứ giác có thể là hình vuông, chữ nhật phải không bạn?
P/s: Hỏi thôi chớ không trả lời đâu :D

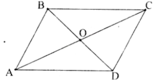
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
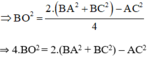
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
bạn vào tìm kiếm là thấy câu hỏi giống bạn thôi bạn xem lời giải là đuọc