Một con lắc lò xo m = 0,25 kg, k = 25 N/m đặt trên mặt phẳng nằm ngang không ma sát. Kéo quả nặng đến vị trí lò xo giãn 5 cm và buông nhẹ. Nếu chọn gốc tọa độ O trùng vị trí cân bằng (VTCB) của quả nặng, chiều dương Ox hướng theo chiều nén của lò xo. Gốc thời gian t = 0 khi vật đi qua VTCB lần đầu tiên, thì phương trình dao động của quả nặng là gì?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kéo quả nặng đến vị trí lò xo giãn 5 cm → A = 5 cm.
Tần số góc ω = Căn (k/m) = Căn (25/0.25) = 10 rad/s.
Tại thời điểm t = 0 vật đi qua vị trí cân bằng lần đầu tiên → φ = -π/2 rad.
→ phương trình dao động của quả nặng là x = 5cos(10t – π/2) cm.

Chọn đáp án A
Để đơn giản, ta có thể xem dao động tắt dần của con lắc là chuỗi các dao động điều hòa mỗi nửa chu kì, với vị trí cân bằng nằm ở hai bên gốc tọa độ O và cách O một đoạn

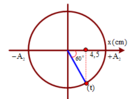

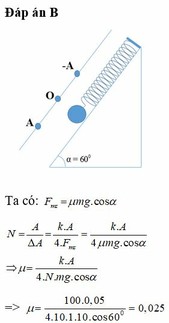
Chọn đáp án B
+ Sau 10 dao động vật dừng lại như vậy có 20 lần qua VTCB
+ Độ giảm biên độ của vật sau một lần qua VTCB:
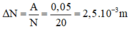
Mặt khác vật dao động tắt dần trên mặt phẳng nghiên nên ta có độ giảm biên độ sau một lần vật qua VTCB:
![]()

Chọn đáp án B
Sau 10 dao động vật dừng lại như vậy có 20 lần qua VTCB
Độ giảm biên độ của vật sau một lần qua VTCB: Δ N = A N = 0 , 05 20 = 2 , 5.10 − 3 m
Mặt khác vật dao động tắt dần trên mặt phẳng nghiên nên ta có độ giảm biên độ sau một lần vật qua VTCB: 2 μ m g cos α k = 2 , 5.10 − 3 ⇒ u = 2 , 5.10 − 2

Đáp án C.
Ta có:
![]()
Độ giảm biên độ trong một chu kì:
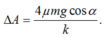
Số dao động từ lúc bắt đầu đến lúc dừng lại:
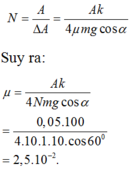

Gọi \(l\) là chiều dài lò xo lúc ko biến dạng \(\Rightarrow\left\{{}\begin{matrix}l_{max}=l+A=30\\l_{min}=l-A=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}l=25cm\\A=5cm\end{matrix}\right.\)
Khi lò xo dài 30cm, tức là vật đang ở biên dương, độ lớn của gia tốc là 8m/s^2\(\Rightarrow\left|a\right|=\omega^2A=800\left(cm/s^2\right)\Leftrightarrow\omega=\sqrt{\dfrac{800}{A}}=\sqrt{\dfrac{800}{5}}=4\pi\left(rad/s\right)\)
Gốc thời gian là lúc vật qua O theo chiều âm, tức là pha ban đầu bằng pi/2
\(\Rightarrow x=5\cos\left(4\pi t+\dfrac{\pi}{2}\right)\left(cm\right)\)
b/ \(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
Nghĩa là khi vật qua vị trí có li độ là \(\left[{}\begin{matrix}x=-2,5cm\\x=2,5cm\end{matrix}\right.\)
c/ Góc vật quay được trong thời gian delta t là: \(\varphi=\omega.\Delta t=4\pi.\Delta t\left(rad\right)\)
Quãng đường lớn nhất đi được khi vật chuyển động xung quanh vtcb
\(S_{max}=2A.\sin\left(2\pi.\Delta t\right)\)
Quãng đường nhỏ nhất đi được khi vật chuyển động xung quang biên
\(S_{min}=2A-2.A\cos\left(2\pi.\Delta t\right)\)
\(\Rightarrow S_{max}-S_{min}=2A\left(\sin\left(2\pi.\Delta t\right)-1+\cos\left(2\pi.\Delta t\right)\right)\)
Xét \(M=\sin\left(2\pi.\Delta t\right)+\cos\left(2\pi.\Delta t\right)=\cos\left(2\pi\Delta t-\dfrac{\pi}{2}\right)+\cos\left(2\pi\Delta t\right)=2\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}+2\pi\Delta t}{2}\right)\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}-2\pi\Delta t}{2}\right)\)
\(M=2\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)\cos\left(\dfrac{\pi}{4}\right)\)
Để \(\left(S_{max}-S_{min}\right)_{max}\Leftrightarrow M_{max}\Leftrightarrow\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow2\pi\Delta t-\dfrac{\pi}{4}=0\Leftrightarrow\Delta t=\dfrac{\pi}{4.2\pi}=\dfrac{1}{8}\left(s\right)\)
d/ Ta thấy vật N luôn dao động vuông pha với vật M
\(\Rightarrow\left(\dfrac{x_M}{A_M}\right)^2+\left(\dfrac{x_N}{A_N}\right)^2=1\Leftrightarrow\left(\dfrac{2,5\sqrt{3}}{5}\right)^2+\left(\dfrac{x_N}{10}\right)^2=1\Leftrightarrow x_N=\pm2,5\left(cm\right)\)
Tính khoảng cách nên ko cần quan tâm xN dương hay âm
\(MN=\sqrt{ON^2+OM^2}=\sqrt{2,5^2+\left(2,5\sqrt{3}\right)^2}=5cm\)

Đáp án C
Hướng dẫn:
Hai vật sẽ tách khỏi nhau khi chúng cùng đi qau vị trí cân bằng. Tần số góc của hệ dao động ω = k 2 m .
→ Tốc độ của vật m tại vị trí hai vật tách nhau v = v m a x = ω A = 8 ω .
+ Biến cố xảy ra chỉ làm thay đổi tần số góc của hệ dao động mà không làm thay đổi vị trí cân bằng của hệ.
→ Tần số góc của hệ dao động lúc sau ω = k m = 2 ω .
→ Biên độ dao động mưới của vật m là A = v m a x ω ' = 8 ω ω ' = 4 2 cm.
+ Năng lượng của hệ E = 0 , 5 k A ' 2 = 16 m J .
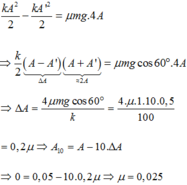
Kéo quả nặng đến vị trí lò xo giãn 5 cm → A = 5 cm.
Tần số góc ω = Căn (k/m) = Căn (25/0.25) = 10 rad/s.
Tại thời điểm t = 0 vật đi qua vị trí cân bằng lần đầu tiên → φ = -π/2 rad.
→ phương trình dao động của quả nặng là x = 5cos(10t – π/2) cm.