Tìm max , min : a) (2x−3)(1+3x) ...
Đọc tiếp
Tìm max , min : a) (2x−3)(1+3x)
b) (1−2x)(1+4x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
1
1 tháng 2 2022
a; \(A=2x+6x^2-3-9x\)
\(=6x^2-7x-3\)
\(=6\left(x^2-\dfrac{7}{6}x-\dfrac{1}{2}\right)\)
\(=6\cdot\left(x^2-2\cdot x\cdot\dfrac{7}{3}+\dfrac{49}{6}-\dfrac{26}{3}\right)\)
\(=6\left(x-\dfrac{7}{3}\right)^2-52\ge-52\forall x\)
Dấu '=' xảy ra khi x=7/3
b: \(B=3+12x-2x-8x^2\)
\(=-8x^2+10x+3\)
\(=-8\left(x^2-\dfrac{5}{4}x-\dfrac{3}{8}\right)\)
\(=-8\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{53}{8}\right)\)
\(=-8\left(x-\dfrac{5}{2}\right)^2+53\le53\forall x\)
Dấu '=' xảy ra khi x=5/2
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Tìm min:
$F=3x^2+x-2=3(x^2+\frac{x}{3})-2$
$=3[x^2+\frac{x}{3}+(\frac{1}{6})^2]-\frac{25}{12}$
$=3(x+\frac{1}{6})^2-\frac{25}{12}\geq \frac{-25}{12}$
Vậy $F_{\min}=\frac{-25}{12}$. Giá trị này đạt tại $x+\frac{1}{6}=0$
$\Leftrightarrow x=\frac{-1}{6}$
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Tìm min
$G=4x^2+2x-1=(2x)^2+2.2x.\frac{1}{2}+(\frac{1}{2})^2-\frac{5}{4}$
$=(2x+\frac{1}{2})^2-\frac{5}{4}\geq 0-\frac{5}{4}=\frac{-5}{4}$ (do $(2x+\frac{1}{2})^2\geq 0$ với mọi $x$)
Vậy $G_{\min}=\frac{-5}{4}$. Giá trị này đạt tại $2x+\frac{1}{2}=0$
$\Leftrightarrow x=\frac{-1}{4}$
KT
16 tháng 8 2018
BÀI 1:
a) \(A=x^2+2x+3=\left(x+1\right)^2+2\ge2\)
Vậy MIN \(A=2\)khi \(x=-1\)
b) \(B=x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Vậy MIN \(B=\frac{3}{4}\)khi \(x=-\frac{1}{2}\)
c) \(C=2x^2+3x-1=2\left(x+\frac{3}{4}\right)^2-\frac{17}{8}\ge-\frac{17}{8}\)
Vậy MIN \(C=-\frac{17}{8}\)khi \(x=-\frac{3}{4}\)
d) \(D=4x^2-x=\left(2x-\frac{1}{4}\right)^2-\frac{1}{16}\ge-\frac{1}{16}\)
Vậy MIN \(D=-\frac{1}{16}\)khi \(x=\frac{1}{8}\)
S
31 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
UN
0
TY
0
HT
1
23 tháng 12 2023
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
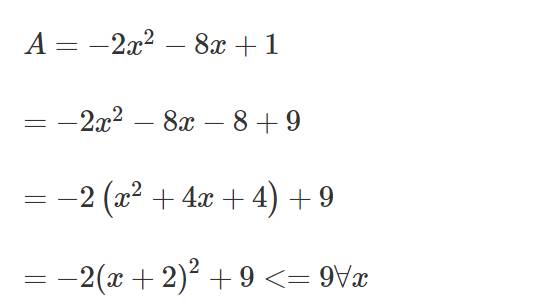
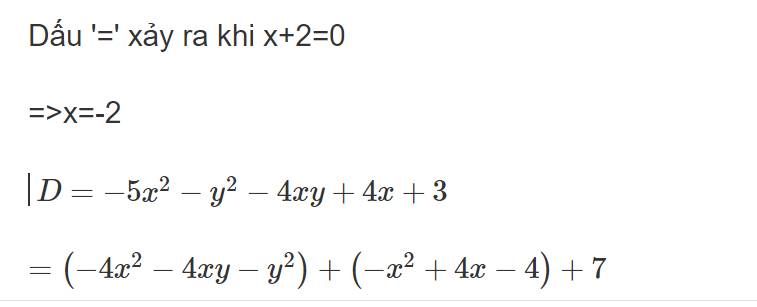
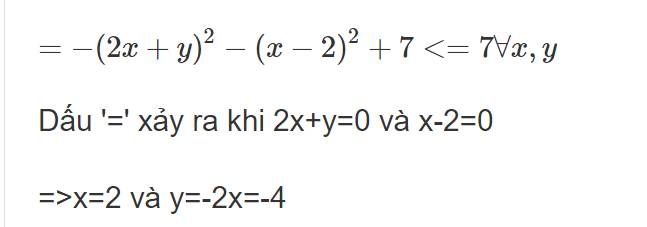
a) Minium: \(-\frac{121}{24}\)
b) Maxium: \(\frac{9}{8}\)
Là sao z bn? Bn có thể làm rõ cho mk dc ko