CM: \(x^2+y^2+z^2+t^2\ge x\left(y+z+t\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
2
8 tháng 8 2016
nhân cả 2 vế với 2 rồi biến đổi tương đương là ra kết quả bạn nhé
HN
2
24 tháng 6 2018
\(x^2+y^2+z^2+t^2+k^2\ge x\left(y+z+t+k\right)\left(1\right)\)
<=>\(4x^2+4y^2+4z^2+4t^2+4k^2-4x\left(y+z+t+k\right)\ge0\)
<=>\(\left(x^2-4xy+4y^2\right)+\left(x^2-4xz+4z^2\right)+\left(x^2-4xt+4t^2\right)+\left(x^2-4xk+4k^2\right)\ge0\)
<=>\(\left(x-2y\right)^2+\left(x-2z\right)^2+\left(x-2t\right)^2+\left(x-2k\right)^2\ge0\left(2\right)\)
bđt (2) luôn đúng với mọi x,y,z nên bđt (1) luôn đúng.
4 tháng 7 2018
Ủng hộ cách khác nehhh ( Nay t rảnh quá làm cho zui thôi)
Áp dụng bđt Cauchy:
\(\dfrac{x^2}{4}+y^2\ge xy\)
\(\dfrac{x^2}{4}+z^2\ge xz\)
\(\dfrac{x^2}{4}+t^2\ge xt\)
\(\dfrac{x^2}{4}+k^2\ge xk\)
Cộng theo vế:
\(x^2+y^2+z^2+t^2+k^2\ge x\left(y+z+t+k\right)\)
13 tháng 4 2023
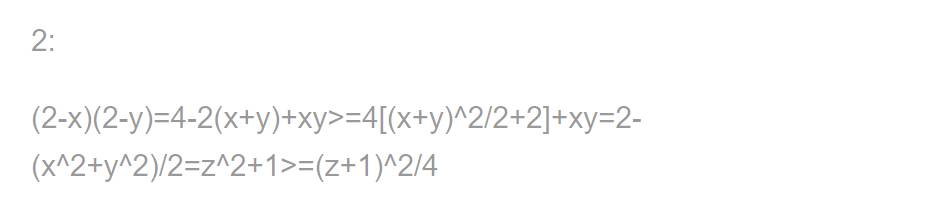
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
18 tháng 5 2023
áp dụng
\(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2};\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{1}{2}.\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\)
\(\Rightarrow A\ge\dfrac{[\left(x+y\right)^2}{2}+z^2].\left(\dfrac{1}{2}.\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2+\dfrac{1}{z^2}\right)\)
áp dụng \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\)
\(\Rightarrow A\ge[\dfrac{\left(x+y\right)^2}{2}+z^2].\left(\dfrac{1}{2}.\left(\dfrac{4}{x+y}\right)^2+\dfrac{1}{z^2}\right)=[\dfrac{\left(x+y\right)^2}{2}+z^2].\left(\dfrac{8}{\left(x+y\right)^2}+\dfrac{1}{z^2}\right)=4+1+\dfrac{\left(x+y\right)^2}{2z^2}+\dfrac{8z^2}{\left(x+y\right)^2}=5+\left(\dfrac{\left(x+y\right)^2}{2z^2}+\dfrac{z^2}{2\left(x+y\right)^2}\right)+\dfrac{15z^2}{2\left(x+y\right)^2}\ge5+2.\sqrt{\dfrac{1}{2}.\dfrac{1}{2}}+\dfrac{15\left(x+y\right)^2}{2.\left(x+y\right)^2}=5+1+\dfrac{15}{2}=\dfrac{27}{2}\)
dbxr<=>y=x=z/2>0
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 12 2018
\(VT=\dfrac{\left(\dfrac{1}{z}\right)^2}{\dfrac{1}{x}+\dfrac{1}{y}}+\dfrac{\left(\dfrac{1}{x}\right)^2}{\dfrac{1}{y}+\dfrac{1}{z}}+\dfrac{\left(\dfrac{1}{y}\right)^2}{\dfrac{1}{x}+\dfrac{1}{z}}\ge\dfrac{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}{2\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)}=\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
Dâu "=" xảy ra khi \(x=y=z\)
HT
22 tháng 7 2020
Hmm, sao ko áp dụng \(\frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c}\ge\frac{\left(x+y+z\right)^2}{a+b+c}\) cho lẹ vậy anh?
\(VT-VP=\left(y^2-xy+\frac{x^2}{4}\right)+\left(z^2-zx+\frac{x^2}{4}\right)+\left(t^2-tx+\frac{x^2}{4}\right)+\frac{x^2}{4}\)
\(=\left(y-\frac{x}{2}\right)^2+\left(z-\frac{x}{2}\right)^2+\left(t-\frac{x}{2}\right)^2+\frac{x^2}{4}\ge0\)
\(\Rightarrow VT\ge VP\)