chỉ cần làm câu 3 ~~~ ~
~
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 4:
b) \(7x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{7}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{y-x}{4-7}=\dfrac{24}{-3}=-8\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-3\right).4=-12\\y=\left(-3\right).7=-28\end{matrix}\right.\)
c) Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{2x}{6}=\dfrac{3y}{12}=\dfrac{2x-3y}{6-12}=\dfrac{24}{-6}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).3=-12\\y=\left(-4\right).4=-16\end{matrix}\right.\)
Bài 3:
a: Ta có: \(\dfrac{2.5}{7.5}=\dfrac{x}{\dfrac{3}{5}}\)
\(\Leftrightarrow\dfrac{x}{\dfrac{3}{5}}=\dfrac{1}{3}\)
hay \(x=\dfrac{1}{5}\)
b: Ta có: \(\dfrac{5}{6}:x=\dfrac{20}{3}\)
\(\Leftrightarrow x=\dfrac{5}{6}:\dfrac{20}{3}=\dfrac{15}{120}=\dfrac{1}{8}\)

Bài 6:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{41}=\dfrac{b}{29}=\dfrac{c}{30}=\dfrac{a+b}{41+29}=\dfrac{700}{70}=10\)
Do đó: a=410; b=290; c=300

Hello teacher
Today I will introduce to you some features of Vietnam
The landscape of Vietnam is rich and beautiful,...
The cuisine is very diverse, rich and eye-catching
costumes, different places will use different traditional costumes.
--end--
đây là bản dịch nha
xin chào thầy
Hôm nay mình sẽ giới thiệu với các bạn một số nét đặc trưng của Việt Nam
Phong cảnh Việt Nam giàu đẹp, ...
Ẩm thực rất đa dạng, phong phú và bắt mắt
trang phục, những nơi khác nhau sẽ sử dụng trang phục truyền thống khác nhau.
--hết--
đây là bản mk tự làm á chứ ko có cop mạng
cậu nhớ tick nhen ;-;

3.
\(D=2\left(x^2+4\right)+\left(y^2+1\right)+\dfrac{28}{x}+\dfrac{1}{y}-9\)
\(D\ge8x+2y+\dfrac{28}{x}+\dfrac{1}{y}-9\)
\(D\ge7\left(x+\dfrac{4}{x}\right)+\left(y+\dfrac{1}{y}\right)+x+y-9\)
\(D\ge14\sqrt{\dfrac{4x}{4}}+2\sqrt{\dfrac{y}{y}}+3-9=24\)
\(D_{min}=24\) khi \(\left(x;y\right)=\left(2;1\right)\)
Bài 4 và 6 trùng nhau?
\(A=\left(\dfrac{3x}{4}+\dfrac{3}{x}\right)+\left(\dfrac{y}{2}+\dfrac{9}{2y}\right)+\left(\dfrac{z}{4}+\dfrac{4}{z}\right)+\dfrac{1}{4}\left(x+2y+3z\right)\)
\(A\ge2\sqrt{\dfrac{9x}{4x}}+2\sqrt{\dfrac{9y}{4y}}+2\sqrt{\dfrac{4z}{4z}}+\dfrac{1}{4}.20\)
\(A\ge13\)
\(A_{min}=13\) khi \(\left(x;y;z\right)=\left(2;3;4\right)\)


a: \(B=\dfrac{16x-x^2-\left(2x+3\right)\left(x+2\right)+\left(3x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{\left(x+2\right)^2}{x-1}\)
\(=\dfrac{16x-x^2-2x^2-7x-6+3x^2-8x+4}{\left(x-2\right)}\cdot\dfrac{x+2}{x-1}\)
\(=\dfrac{x-2}{\left(x-2\right)}\cdot\dfrac{x+2}{x-1}=\dfrac{x+2}{x-1}\)
b: Để B=1/2 thì \(\dfrac{x+2}{x-1}=\dfrac{1}{2}\)
=>2x+4=x-1
=>x=-5

a/
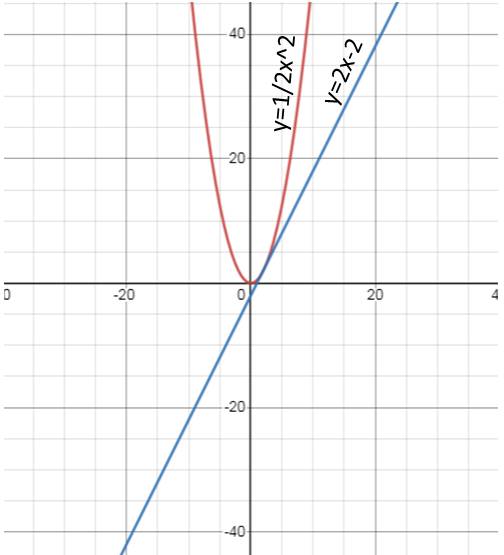
b/
Tọa độ giao điểm của 2 đồ thị là:
\(\dfrac{1}{2}x^2=2x-2\\ \Leftrightarrow\dfrac{1}{2}x^2-2x+2=0\\ \Leftrightarrow x=2\)
b) Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = 2x - 2
⇔x² = 4x - 4
⇔x² - 4x + 4 = 0
⇔(x - 2)² = 0
⇔x - 2 = 0
⇔x = 2
⇔y = 2.2 - 2 = 2
Vậy tọa độ giao điểm của (P) và (d) là (2;2)


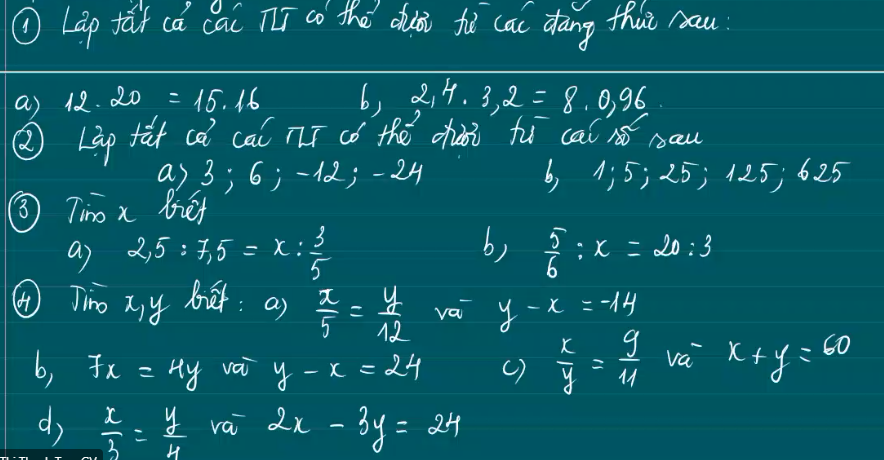

 mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17
mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17 chỉ cần làm câu 3,4,5,6
chỉ cần làm câu 3,4,5,6
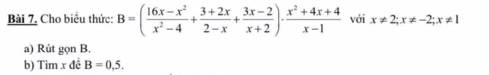
 giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
A B M C D I K H x y K'
Kẻ hình phụ và các điểm như hình trên. (chú ý CK' , IH , DK vuông góc với AB)
Dễ dàng chứng minh được IK và IK' lần lượt là các đường trung bình của hình thang CDBM và CDMA => K, K' cố định
=> \(\begin{cases}IK=\frac{1}{2}\left(CM+BD\right)\\IK'=\frac{1}{2}\left(AC+MD\right)\end{cases}\)
\(\Rightarrow IK=IK'=\frac{1}{2}AB\) không đổi
Vì IK // BD nên góc DBA = góc IKA = 60 độ
=> tam giác IKK' là tam giác đều có cạnh không đổi
Từ I kẻ đường cao IH => H là trung điểm AB =>H cố định (1) . Đặt AB = a
\(\Rightarrow IH^2=IK^2-\left(\frac{IK}{2}\right)^2=\left(\frac{a}{2}\right)^2-\left(\frac{a}{4}\right)^2=\frac{3a^2}{16}\Rightarrow IH=\frac{a\sqrt{3}}{4}\)(2) không đổi
Suy ra \(I\in\left(H;\frac{a\sqrt{3}}{4}\right)\) hay tập hợp quỹ tích điểm I thuộc đường tròn tâm H bán kính \(\frac{a\sqrt{3}}{4}\)
Quí tích ?