Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi M là gđ của tia pg ở C với AB, N là gđ của tia pg ở B với AC.
*Tính góc BIC:
Xét tam giác BIC: BIC = 180 - ( IBC + ICB )
Xét tam giác ABC: A + ABC + ACB = 180 <=> A + 2IBC + 2ICB = 180 <=> A + 2(IBC + ICB) = 180
<=> IBC + ICB = (180 - α ) : 2
Từ đây em tính đc góc BIC
*Tính góc BKC:
Em nhìn vào tứ giác BICK. Trong 1 tứ giác thì tổng các góc bằng 360 độ.
Gọi 2 góc phân giác ngoài ở B là B1, B2; tương tự có C1, C2.
Ta có: ABC + B1 + B2 = 180 <=> 2IBC + 2B1 (CBK) = 180 <=> IBC + B1 = 90 <=> IBC = 90
Tương tự: ACB + C1 + C2 = 180 <=> 2ICB + 2C1 (BCK) = 180 <=> ICB + C1 = 90 <=> ICK = 90
Xét tứ giác BICK: BIC + IBK + BKC + ICK = 360
Có 3 góc rồi em sẽ tính đc BKC
*Tính góc BEC:
Xét tam giác BEK: BEC + EBK + BKC = 180
Đã có EBK và BKC => BEC
cách 2
Góc ABC + góc ACB=180 độ-α => góc IBC+góc ICB=(ABC + góc ACB)/2=(180 độ-α)/2
=> góc BIC=180 độ - (góc IBC+góc ICB)=180 độ - (180 độ-α)/2 = 90 độ+α/2
_Vì mỗi góc, tia phân giác trong luôn vuông góc với tia phân giác ngoài nên
Xét tứ giác BICK có tổng số đo các góc là 360 độ, góc B và góc C vuông
=>góc BKC=360 - (góc IBK+góc ICK) - góc BIC=360-90.2- (90 độ+α/2)=90 độ - α/2
_Góc BEC= 180 độ - góc IBK - góc BKC= 180 - 90 - (90 độ - α/2) = α/2
Gọi M là gđ của tia pg ở C với AB, N là gđ của tia pg ở B với AC.
*Tính góc BIC:
Xét tam giác BIC: BIC = 180 - ( IBC + ICB )
Xét tam giác ABC: A + ABC + ACB = 180 <=> A + 2IBC + 2ICB = 180 <=> A + 2(IBC + ICB) = 180
<=> IBC + ICB = (180 - α ) : 2
Từ đây em tính đc góc BIC
*Tính góc BKC:
Em nhìn vào tứ giác BICK. Trong 1 tứ giác thì tổng các góc bằng 360 độ.
Gọi 2 góc phân giác ngoài ở B là B1, B2; tương tự có C1, C2.
Ta có: ABC + B1 + B2 = 180 <=> 2IBC + 2B1 (CBK) = 180 <=> IBC + B1 = 90 <=> IBC = 90
Tương tự: ACB + C1 + C2 = 180 <=> 2ICB + 2C1 (BCK) = 180 <=> ICB + C1 = 90 <=> ICK = 90
Xét tứ giác BICK: BIC + IBK + BKC + ICK = 360
Có 3 góc rồi em sẽ tính đc BKC
*Tính góc BEC:
Xét tam giác BEK: BEC + EBK + BKC = 180
Đã có EBK và BKC => BEC
cách 2
Góc ABC + góc ACB=180 độ-α => góc IBC+góc ICB=(ABC + góc ACB)/2=(180 độ-α)/2
=> góc BIC=180 độ - (góc IBC+góc ICB)=180 độ - (180 độ-α)/2 = 90 độ+α/2
_Vì mỗi góc, tia phân giác trong luôn vuông góc với tia phân giác ngoài nên
Xét tứ giác BICK có tổng số đo các góc là 360 độ, góc B và góc C vuông
=>góc BKC=360 - (góc IBK+góc ICK) - góc BIC=360-90.2- (90 độ+α/2)=90 độ - α/2
_Góc BEC= 180 độ - góc IBK - góc BKC= 180 - 90 - (90 độ - α/2) = α/2
Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ
a/ Xét tg BIC có
\(\widehat{BIC}=180^o-\left(\widehat{IBC}+\widehat{ICB}\right)=180^o-\dfrac{\widehat{B}}{2}-\dfrac{\widehat{C}}{2}=\)
\(=180^o-\left(\dfrac{\widehat{B}+\widehat{C}}{2}\right)=180^o-\left[\dfrac{180^o-\widehat{A}}{2}\right]=90^o+\dfrac{\widehat{A}}{2}\left(dpcm\right)\)
b/ Để c/m câu này ta chứng minh bài toán phụ: " Hai đường phân giác ngoài của 2 góc với đường phân giác trong của góc còn lại đồng quy"
Có hai đường phân giác của các góc ngoài của góc B và góc C cắt nhau tại J.
Từ J dựng các đường vuông góc với AB; AC; BC cắt 3 cạnh trên lần lượt tại D; E; F
Vì J thuộc đường phân giác của \(\widehat{DBC}\) nên JD=JF
Vì J thuộc đường phân giác của \(\widehat{ECB}\) nên JE=JF
(Mọi điểm thuộc đường phân giác của một góc thì cách đều hai cạnh của góc)
=> JD=JE
Xét tg vuông ADJ và tg vuông AEJ có
ẠJ chung; JD=JE (cmt) => tg ADJ = tg AEJ (hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{DAJ}=\widehat{EAJ}\) => Ạ là phân giác của góc \(\widehat{BAC}\)
Áp dụng vào bài toán:
Nối AJ => AJ là phân giác của \(\widehat{BAC}\) => AJ phải đi qua I (Trong tg 3 đường phân giác trong đồng quy) => A; I; J thẳng hàng
c/ Vì J; H; K bình đẳng nên B; I; K thẳng hàng và C; I; H thẳng hàng
=> AJ; BK; CH đồng quy tại I
Kẻ IH ⊥ AB, IJ ⊥ BC, IG ⊥ AC, KD ⊥ AB, KE ⊥ AC, KF ⊥ BC
Vì I nằm trên tia phân giác của ∠(BAC) nên IH = IG (tính chất tia phân giác)
Vì I nằm trên tia phân giác của ∠(BCA) nên IJ = IG (tính chất tia phân giác)
Suy ra: IH = IJ
Do đó I nằm trên tia phân giác của ∠(ABC) (1)
Vì K nằm trên tia phân giác của ∠(DAC) nên KD = KE (tính chất tia phân giác)
Vì K nằm trên tia phân giác của ∠(ACF) nên KE = KF (tính chất tia phân giác)
Suy ra: KD = KF
Do đó K nằm trên tia phân giác của ∠(ABC) (2)
Từ (1) và (2) suy ra: B, I, K thẳng hàng.
Lời giải:
Kẻ $KM, KT, KN$ lần lượt vuông góc với $AB, AC, BC$.
Vì $K$ thuộc tia phân giác $\widehat{MAC}$ nên $KM=KT$ (tính chất quen thuộc)
Vì $K$ thuộc tia phân giác $\widheat{ACN}$ nên $KN=KT$
$\Rightarrow KM=KN$
$\Rightarrow K$ thuộc tia phân giác $\widehat{MBN}$ hay $\widehat{ABC}$
Do đó $BI, BK$ cùng là tia phân giác $\widehat{ABC}$
$\Rightarrow B,I,K$ thẳng hàng
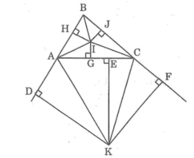
a) Ta có :
Góc B1 + Góc B2 = 180o
\(\Rightarrow\frac{1}{2}\)Góc B1 + \(\frac{1}{2}\)Góc B2 = 90o
\(\Rightarrow\)Góc ABx + Góc ABI = 90o
\(\Rightarrow\)Góc IBx = 90o
Mà góc IBx + góc IBK = 180o ( kề bù )
\(\Rightarrow\)Góc IBK = 90o ; nên \(\Delta IBK\) vuông tại B.
Chứng minh tương tự, ta cũng có góc ICK vuông, nên \(\Delta ICK\)vuông tại C.
b) Ta có :
Góc B + Góc C = \(180^o-\)Góc A
\(\Rightarrow2.\)Góc C + Góc C = 180o - \(\alpha\)
Góc C = \(\frac{180^o-\alpha}{3}=60^o-\frac{\alpha}{3}\)
Góc B = \(\left(60^o-\frac{\alpha}{3}\right).2=120^o-\frac{2\alpha}{3}\)
thank