\(\text{Giải bài toán bằng cách lập phương trình:}\)
Một ca nô xuôi dòng từ A->B hết 5h rồi ngược dòng từ B->A hết 8h.Tính vận tốc thực của ca nô và quãng đường AB biết vận tốc dòng nước là 3km/h
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 9 2019
Đổi 7 giờ 30 phút =15/2 (h)
Gọi vận tốc thực của ca nô là x (km/h), x > 3
Vận tốc của ca nô khi xuôi dòng sông từ A đến B là x + 3 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là x – 3 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là 54/(x+3) (h)
Thời gian của ca nô khi ngược dòng song từ B về A là 54/(x-3) (h)
Do ca nô chạy xuôi dòng từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:
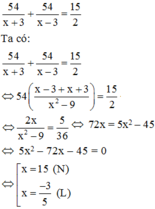
Vậy vận tốc thực của ca nô là 15 (km/h)
Đáp án: D
AH
Akai Haruma
Giáo viên
9 tháng 6 2021
Bạn lưu ý đăng bài đúng lớp. Bài này cần sử dụng kiến thức từ lớp 8 trở lên chứ không phải bài lớp 5.
AH
Akai Haruma
Giáo viên
9 tháng 6 2021
Lời giải:
Gọi vận tốc thực của cano là $a$ (km/h). ĐK: $a>3$
Vận tốc xuôi dòng: $a+3$ km/h
Vận tốc ngược dòng: $a-3$ km/h
Ta có:
$\frac{36}{a+3}+\frac{36}{a-3}=5$ (giờ)
Giải pt này ta thu được $a=15$ là giá trị duy nhất thỏa mãn
Vậy vận tốc thực là $15$ km/h
XO
9 tháng 6 2021
Gọi vận tốc của cano là x (km/h) (x > 3)
Ta có : Vận tốc xuôi của ca nô : x + 3 (km/h)
vận tốc ngược của ca nô : x - 3 (km/h)
=> Thời gian xuôi : \(\frac{36}{x+3}\)(h)
Thời gian ngược \(\frac{36}{x-3}\left(h\right)\)
mà tổng thời gian đi là 5 giờ
=> Ta có phương trình \(\frac{36}{x+3}+\frac{36}{x-3}=5\)
=> \(\frac{36\left(x-3\right)+36\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\frac{5\left(x+3\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}\)
=> 72x = 5(x2 - 9)
<=> 5x2 - 72x - 45 = 0
<=> 5(x2 + 72/5x - 9) = 0
=> x2 + 72/5x - 9 = 0
<=> \(x^2-2.\frac{36}{5}x+\frac{1296}{25}-\frac{1521}{25}=0\)
<=> \(\left(x-\frac{36}{5}\right)^2-\left(\frac{39}{5}\right)^2=0\)
<=> \(\left(x+\frac{3}{5}\right)\left(x-15\right)=0\)
<=> \(\orbr{\begin{cases}x=-\frac{3}{5}\left(\text{loại}\right)\\x=15\left(tm\right)\end{cases}}\)
Vậy vận tốc thử của ca nô là 15km/h
QA
9 tháng 6 2021
Trả lời:
Gọi vận tốc thực của cano là x ( km/h; x > 3 )
=> Vận tốc của cano lúc xuôi dòng là: x + 3 (km/h)
Thời gian cano đi từ A đến B là: \(\frac{36}{x+3}\)(giờ)
Vân tốc của cano lúc ngược dòng là: x - 3 (km/h)
Thời gian cano đi từ B về A là: \(\frac{36}{x-3}\)(giờ)
Theo bài ra ta có phương trình:
\(\frac{36}{x+3}+\frac{36}{x-3}=5\)
\(\Rightarrow\frac{36\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}+\frac{36\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{5\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow36\left(x-3\right)+36\left(x+3\right)=5\left(x-3\right)\left(x+3\right)\)
\(\Leftrightarrow36x-108+36x+108=5\left(x^2-9\right)\)
\(\Leftrightarrow72x=5x^2-45\)
\(\Leftrightarrow5x^2-72x-45=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=15\left(tm\right)\\x=\frac{-3}{5}\left(ktm\right)\end{cases}}\)
Vậy vận tốc thực của cano là: 15 km/h
18 tháng 3 2022
Gọi vận tốc thực là x(km/h) x>0
Vận tốc xuôi:x+3(km/h)
Vận tốc ngược:x-3(km/h)
Thời gian đi từ xuôi dòng : \(\dfrac{48}{x+3}\)( h)
Thời gian đi ngược dòng: \(\dfrac{48}{x-3}\)(h)
Theo bài ra ta có pt
\(\dfrac{48}{x-3}\)+\(\dfrac{48}{x+3}\)+\(\dfrac{20}{60}\)=7
Giải ra được x=15(tm)
Vậy....
A
16 tháng 1 2020
Gọi vận tốc ca nô là x
Gọi vận tốc dòng nước là y (đơn vị km/h ; x,y > 0 )
Theo đề ta có
vận tốc khi xuôi dòng : x + y
vận tốc khi ngược dòng : x - y
2h30p=2.5h=5/2h
1h20p=4/3h
\(\frac{S}{v_{xuôi}}+\frac{S}{v_{ngược}}=\frac{12}{x+y}+\frac{12}{x-y}=\frac{5}{2}\)
\(\frac{4}{x+y}+\frac{8}{x-y}=\frac{4}{3}\)
Từ trên ta có HPT \(\hept{\begin{cases}\frac{12}{x+y}+\frac{12}{x-y}=\frac{5}{2}\\\frac{4}{x+y}+\frac{8}{x-y}=\frac{4}{3}\end{cases}}\)
Gọi \(x+y=a;x-y=b\)
\(\Leftrightarrow\hept{\begin{cases}\frac{12}{a}+\frac{12}{b}=\frac{5}{2}\\\frac{4}{a}+\frac{8}{b}=\frac{4}{3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{12}{a}+\frac{12}{b}=\frac{5}{2}\\\frac{12}{a}+\frac{24}{b}=\frac{12}{3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{12}{b}=\frac{3}{2}\\\frac{12}{a}+\frac{24}{b}=\frac{12}{3}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=8\\\frac{12}{a}+\frac{24}{8}=\frac{12}{3}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=8\\a=12\end{cases}}\)
\(\Rightarrow b=x-y=8;a=x+y=12\)
\(\Rightarrow x=10;y=2\)
PT Trên có 1 nghiệm (x;y) = (10;2 )
22 tháng 3 2021
Gọi vận tốc cano là $x(km;x>0)$
Quãng đường từ $A$ đến $B$ sẽ là: $3(x+2)(km)$
Quãng đường từ $B$ về $A$ sẽ là: $3\dfrac{1}{3}.(x-2)(km)$
Nên ta sẽ có phương trình:
$3(x+2)=3\dfrac{1}{3}.(x-2)$
$⇔3x+6=\dfrac{10(x-2)}{3}$
$⇔9x+18=10x-20$
$⇔x=38(km/h)$
Nên quãng đường $AB$ là: $3.(x+2)=3.(38+2)=120(km)$
Gọi vận tốc thực cano là x
Theo đề, ta có: 5(x+3)=8(x-3)
=>5x+15=8x-24
=>-3x=-39
=>x=13
Độ dài quãng đường AB là 5(13+3)=80km