Rút gọn biểu thức: \(\frac{2a+\sqrt{ab}-3b}{2a-5\sqrt{ab}+3b}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
17 tháng 6 2020
\(M=\frac{2\sqrt{a}\left(\sqrt{a}+\sqrt{2a}-\sqrt{3b}\right)+\sqrt{3b}\left(2\sqrt{a}-\sqrt{3b}\right)-2a\sqrt{a}}{a\sqrt{2}+\sqrt{3ab}}\left(đkxđ:a,b\ge0;mau\ne0\right)\)[tự tìm cái sau :)) ]
\(VP=\frac{2\sqrt{a}\left(\sqrt{a}+\sqrt{2}.\sqrt{a}-\sqrt{3}.\sqrt{b}\right)}{a\sqrt{2}+\sqrt{3ab}}+\frac{\sqrt{3b}\left(2\sqrt{a}-\sqrt{3b}\right)}{a\sqrt{2}+\sqrt{3ab}}-\frac{2a\sqrt{a}}{a\sqrt{2}+\sqrt{3ab}}\)
\(=\frac{2a+2a\sqrt{2}-2\sqrt{3ab}}{a\sqrt{2}+\sqrt{3ab}}+\frac{2\sqrt{3ab}-3b}{a\sqrt{2}+\sqrt{3ab}}-\frac{2a\sqrt{a}}{a\sqrt{2}+\sqrt{3ab}}\)
\(=\frac{2a+2a\sqrt{2}-3b+2a\sqrt{a}}{a\sqrt{2}+\sqrt{3ab}}\)
mình làm được đến đây , bạn làm được tiếp thì làm =))
DA
2
10 tháng 8 2021
\(\dfrac{2a+\sqrt{ab}-3b}{2a-5\sqrt{ab}+3b}\\ =\dfrac{2a-2\sqrt{ab}+3\sqrt{ab}-3b}{2a-2\sqrt{ab}-3\sqrt{ab}+3b}\\ =\dfrac{2\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)+3\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{2\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)-3\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}\\ =\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(2\sqrt{a}+3\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(2\sqrt{a}-3\sqrt{b}\right)}\\ =\dfrac{2\sqrt{a}+3\sqrt{b}}{2\sqrt{a}-3\sqrt{b}}\)
Tick nha
29 tháng 6 2019
\(=\frac{\left(\sqrt{a}-\sqrt{b}\right)^3+2\sqrt{a^3}+\sqrt{b^3}}{3\sqrt{a}\left(\sqrt{a^3}+\sqrt{b^3}\right)}+\frac{\sqrt{a}\left(\sqrt{b}-\sqrt{a}\right)}{\sqrt{a}\left(a-b\right)}\)
\(=\frac{\sqrt{a^3}-3a\sqrt{b}+3\sqrt{a}.b-\sqrt{b^3}+2\sqrt{a^3}+\sqrt{b^3}}{3\sqrt{a}\left(\sqrt{a^3}+\sqrt{b^3}\right)}+\frac{\sqrt{a}\left(\sqrt{b}-\sqrt{a}\right)}{\sqrt{a}\left(a-b\right)}\)
\(=\frac{3\sqrt{a^3}-3a\sqrt{b}+3b\sqrt{a}}{3\sqrt{a}\left(\sqrt{a^3}+\sqrt{b^3}\right)}+\frac{\sqrt{a}\left(\sqrt{b}-\sqrt{a}\right)}{\sqrt{a}\left(a-b\right)}\)
\(=\frac{a-\sqrt{ab}+b}{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}-\frac{1}{\sqrt{a}+\sqrt{b}}=0\)
17 tháng 9 2018
\(\dfrac{2a+\sqrt{ab}-3b}{2a-5\sqrt{ab}+3b}=\dfrac{2a-2\sqrt{ab}+3\sqrt{ab}-3b}{2a-2\sqrt{ab}-3\sqrt{ab}+3b}\)
\(=\dfrac{2\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)+3\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{2\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)-3\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(2\sqrt{a}+3\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(2\sqrt{a}-3\sqrt{b}\right)}\)
\(=\dfrac{2\sqrt{a}+3\sqrt{b}}{2\sqrt{a}-3\sqrt{b}}\)
17 tháng 9 2018
\(ĐK:a,b\ge0;a\ne b.\dfrac{2a+\sqrt{ab}-3b}{2a-5\sqrt{ab}+3b}=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(2\sqrt{a}+3\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(2\sqrt{a}-3\sqrt{b}\right)}=\dfrac{2\sqrt{a}+3\sqrt{b}}{2\sqrt{a}-3\sqrt{b}}\)
NN
3
23 tháng 7 2021
A = (-2a + 3b - 4c) - (-2a - 3b - 4c)
= -2a + 3b - 4c +2a + 3b + 4c
=6b
AH
Akai Haruma
Giáo viên
24 tháng 2 2020
Bài 1:
$14+\sqrt{40}+\sqrt{56}+\sqrt{140}=14+\sqrt{56}+(\sqrt{40}+\sqrt{140})$
=14+2\sqrt{10}+2\sqrt{14}+2\sqrt{35}=(12+2\sqrt{35})+2+(2\sqrt{10}+2\sqrt{14})$
$=(\sqrt{5}+\sqrt{7})^2+2+2\sqrt{2}(\sqrt{5}+\sqrt{7})$
$=(\sqrt{5}+\sqrt{7}+\sqrt{2})^2$
$\Rightarrow \sqrt{14+\sqrt{40}+\sqrt{56}+\sqrt{140}}=\sqrt{2}+\sqrt{5}+\sqrt{7}$
\(\Rightarrow A=\frac{\sqrt{2}+\sqrt{5}+\sqrt{7}}{\sqrt{2}+\sqrt{5}+\sqrt{7}}=1\)
AH
Akai Haruma
Giáo viên
24 tháng 2 2020
Lời giải:
a) ĐKXĐ: $a,b\geq 0$ và $a,b$ không đồng thời cùng bằng $0$
\(B=\frac{2a+2\sqrt{2}a-2\sqrt{3ab}+2\sqrt{3ab}-3b-2a\sqrt{2}}{a\sqrt{2}+\sqrt{3ab}}=\frac{2a-3b}{\sqrt{a}(\sqrt{2a}+\sqrt{3b})}=\frac{(\sqrt{2a}-\sqrt{3b})(\sqrt{2a}+\sqrt{3b})}{\sqrt{a}(\sqrt{2a}+\sqrt{3b})}\)
\(=\frac{\sqrt{2a}-\sqrt{3b}}{\sqrt{a}}=\sqrt{2}-\sqrt{\frac{3b}{a}}\)
b)
\(a=1+3\sqrt{2}; 3b=30+11\sqrt{8}\Rightarrow \frac{3b}{a}=\frac{30+11\sqrt{8}}{1+3\sqrt{2}}=\frac{(30+11\sqrt{8})(1-3\sqrt{2})}{(1+3\sqrt{2})(1-3\sqrt{2})}\)
\(=\frac{102+68\sqrt{2}}{17}=6+4\sqrt{2}=(2+\sqrt{2})^2\)
\(\Rightarrow \sqrt{\frac{3b}{a}}=2+\sqrt{2}\)
\(\Rightarrow B=\sqrt{2}-(2+\sqrt{2})=-2\)
28 tháng 6 2019
\(S=\frac{\left[\frac{\left(a-b\right)\left(\sqrt{a}-\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\right]^3+2a\sqrt{a}+b\sqrt{b}}{3a^2+3b\sqrt{ab}}+\frac{\sqrt{a}\left(\sqrt{b}-\sqrt{a}\right)}{\sqrt{a}\left(a-b\right)}\)
\(S=\frac{\left(\sqrt{a}-\sqrt{b}\right)^3+2\left(\sqrt{a}\right)^2\sqrt{a}+\left(\sqrt{b}\right)^2\sqrt{b}}{3a^2+3b\sqrt{ab}}+\frac{\sqrt{b}-\sqrt{a}}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(S=\frac{\left(\sqrt{a}\right)^3-3\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)-\left(\sqrt{b}\right)^3+2\left(\sqrt{a}\right)^3+\left(\sqrt{b}\right)^3}{3a^2+3b\sqrt{ab}}-\frac{1}{\sqrt{a}+\sqrt{b}}\)
\(S=\frac{3\left(\sqrt{a}\right)^3-3a\sqrt{b}+3\sqrt{a}b}{3a^2+3b\sqrt{ab}}-\frac{1}{\sqrt{a}+\sqrt{b}}\)
\(S=\frac{\sqrt{a}\left(a-\sqrt{ab}+b\right)}{\sqrt{a}\left[\left(\sqrt{a}\right)^3+\left(\sqrt{b}\right)^3\right]}-\frac{1}{\sqrt{a}+\sqrt{b}}\)
\(S=\frac{a-\sqrt{ab}+b}{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}-\frac{1}{\sqrt{a}+\sqrt{b}}\)
\(S=\frac{1}{\sqrt{a}+\sqrt{b}}-\frac{1}{\sqrt{a}+\sqrt{b}}=0\)
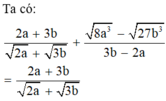
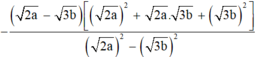
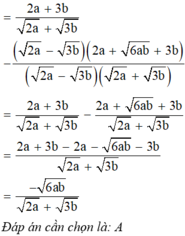
\(=\frac{2a-2\sqrt{ab}+3\sqrt{ab}-3b}{2a-2\sqrt{ab}-3\sqrt{ab}+3b}=\frac{2\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)+3\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{2\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)-3\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\frac{\left(2\sqrt{a}+3\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\left(2\sqrt{a}-3\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\frac{2\sqrt{a}+3\sqrt{b}}{2\sqrt{a}-3\sqrt{b}}\)