Cho ΔABC vuông tại A, đường cao AH. Gọi trung điểm của BH là P, trung điểm cả AH là Q. Cmr:
a, ΔABP đồng dạng với ΔCAQ
b, ΔHCQ đồng dạng với ΔHAP
c, AP vuông góc với CQ
Các bạn giúp mình với, mình đang cần rất gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
30 tháng 3 2021
Bài giải
a) Xét tam giác ABH và CAH có:
\(\widehat{AHB}=\widehat{CHA}\left(=90^o\right)\)
\(\widehat{BAH}=\widehat{ACH}\left(=90^o-\widehat{ABC}\right)\)
\(\Rightarrow\Delta ABH\infty\Delta CAH\left(g.g\right)\)
\(\Delta ABH\infty\Delta CAH\left(g.g\right)\) (câu a) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{BH}{AH}=\dfrac{BH\text{ : }2}{AH\text{ : 2}}=\dfrac{BP}{AQ}\)
Xét \(\Delta ABP \text{và }\Delta CAQ\) có:
\(\widehat{CAH}=\widehat{ABH}\left(=90^o-\widehat{BAH}\right)\)
\(\Rightarrow\Delta ABP\infty\Delta CAQ\left(c.g.c\right)\)
b, Ta có: PQ là đg trung bình của\(\Delta ABH\Rightarrow\text{ }PQ\text{ // }AB\text{ }\Rightarrow\text{ }PQ\perp AC\)
Mà AHPC => Q là trực tâm của \(\Delta APC\)
\(\Rightarrow\text{ }AP\perp CQ\)
24 tháng 8 2021
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC
17 tháng 4 2020
Bài làm
b) Xét tam giác HAP có:
Q là trung điểm BH
P là trung điểm AH
=> QP là đường trung bình
=> QP // AB
=> \(\widehat{HQP}=\widehat{QPA}\)
Xét tam giác HQP và tam giác ABC có:
\(\widehat{HQP}=\widehat{QPA}\)
\(\widehat{PHQ}=\widehat{BAC}\left(=90^0\right)\)
=> Tam giác HQP ~ Tam giác ABC ( g - g )
=> \(\frac{HQ}{AB}=\frac{HP}{AC}\Rightarrow\frac{AC}{AB}=\frac{HP}{HQ}\Rightarrow\frac{AB}{AC}=\frac{HQ}{HP}\) (1)
Xét tam giác HAB có:
QP // AB
=> Tam giác HQP ~ HAB
=> \(\frac{HQ}{QB}=\frac{HP}{PA}\Rightarrow\frac{HQ}{HP}=\frac{QB}{PA}\) (2)
Từ (1) và (2) => \(\frac{AB}{AC}=\frac{QB}{PA}\)
Xét tam giác AHC vuông ở H có:
\(\widehat{PAC}+\widehat{BCA}=90^0\)(3)
Xét tam giác ABC vuông ở A có:
\(\widehat{CBA}+\widehat{BCA}=90^0\) (4)
Từ (3) và (4) => \(\widehat{PAC}=\widehat{CBA}\)
Xét tam giác ABQ và tam giác CAP có:
\(\frac{AB}{AC}=\frac{QB}{PA}\)
\(\widehat{PAC}=\widehat{CBA}\)
=> Tam giác ABQ ~ Tam giác CAP ( c-g-c ) ( đpcm )
17 tháng 4 2020
Bài làm
a) Vì AM là trung tuyến
=> M là trung điểm BC
=> BM = MC = BC/2 = ( BH + HC )/2 = ( 9 + 16 )/2 = 12,5 ( cm )
Ta có: BH + HM + MC = BC
=> BH + HM + MC = BH + HC
hay 9 + HM + 12,5 = 9 + 16
=> HM = 9 + 16 - 9 - 12,5
=> HM = 3,5 ( cm )
Vì tam giác ABC là tam giác vuông ở A
Mà AM trung tuyến
=> AM = MC = BM = 12,5 ( cm )
Xét tam giác AHM vuông ở H có:
Theo định lí Pytago có:
AH2 = AM2 - HM2
hay AH2 = 12,52 - 3,52
=> AH2 = 156,25 - 12,25
=> AH2 = 144
=> AH = 12 ( cm )
SABC = 1/2 . AH . HM = 1/2 . 12 . 3,5 = 21 ( cm2 )
Xét tam giác AHB vuông ở H có:
Theo định lí Py-ta-go có:
AB2 = BH2 + AH2
=> AB2 = 92 + 212
=> AB2 = 81 + 441
=> AB2 = 522
=> AB \(\approx\)22,8 ( cm )
Xét tam giác AHC vuông ở H có:
Theo định lí Pytago có:
AC2 = AH2 + HC2
=> AC2 = AH2 + ( HM + MC )2
hay AC2 = 212 + ( 3,5 + 12,5 )2
=> AC2 = 441 + 256
=> AC2 = 697
=> AC \(\approx\)26,4 ( cm )
Chu vi tam giác ABC là: AB + AC + BC = 22,8 + 26,4 + 25 = 74,2 ( cm )
SABC = 1/2 . AH . BC = 1/2 . 21 . 25 = 262,5 ( cm2 )
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 4 2023
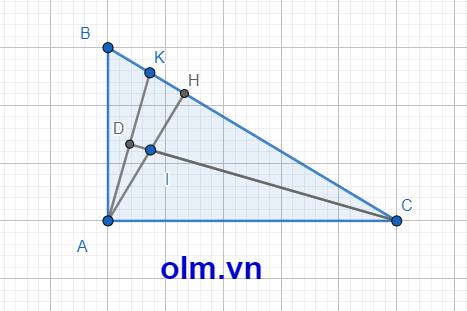
Xét \(\Delta\) HBA và \(\Delta\) ABC có \(\widehat{H}\) = \(\widehat{A}\) = 900; \(\widehat{B}\) chung
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) ABC (g-g)
Tương tự ta có: \(\Delta\) HAC \(\sim\) \(\Delta\) ABC (g-g-g)
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) HAC ( t/c hai tam giác đồng dạng)
⇒ \(\dfrac{HB}{HA}\) = \(\dfrac{HA}{HC}\) = \(\dfrac{BA}{AC}\)( theo khái niệm của tam giác đồng dạng.)
Mặt khác: KI là đường trung bình của tam giác ABH nên:
\(\dfrac{HI}{HA}\) = \(\dfrac{HK}{HB}\) ⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HB}{HA}\)
⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HA}{HC}\) mà \(\widehat{AHK}\) = \(\widehat{CHI}\) = 900
⇒ \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ( c-g-c)
b, Kéo dài CI cắt AK tại D ta có:
vì \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ⇒ \(\widehat{HAK}\) = \(\widehat{HCI}\)
Xét \(\Delta\) HAK và \(\Delta\) DCK có: \(\widehat{A}\) = \(\widehat{C}\) ( cmt)
\(\widehat{K}\) chung
⇒ \(\Delta\) HAK \(\sim\) \(\Delta\) DCK ( g-g)
⇒ \(\widehat{H}\) = \(\widehat{D}\)= 900 ⇒ AK \(\perp\) CI tại D ( đpcm)
a) Dễ dàng cm được : tam giác HBA đồng dạng với tam giác HAC (g.g)
=> \(\frac{HB}{AH}=\frac{AB}{AC}\) hay \(\frac{\frac{BH}{2}}{\frac{AH}{2}}=\frac{AB}{AC}\) hay \(\frac{BP}{AQ}=\frac{AB}{AC}\) ; góc ABC = góc HAC
=> tam giác PBA đồng dạng với tam giác QAC (c.g.c)
b) Vì tam giác ABP đồng dạng với tam giác CAQ nên góc APB = góc AQC
=> góc APC = góc CQH (góc ngoài)
Lại có góc QHC = góc QHP = 90 độ
=> tam giác HQC đồng dạng với tam giác HPA (g.g)
c) Vì tam giác ABP đồng dạng với tam giác CAQ nên góc BAP = góc ACQ
Lại có góc BAP + góc PAC = 90 độ
=> góc ACQ + góc PAC = 90 độ
=> AP vuông góc với CQ