Một vật dao động điều hoà dọc theo trục Ox. Lúc vật qua vị trí có li độ (cm) thì có vận tốc (cm/s) và gia tốc (cm/s2). Chọn gốc toạ độ ở vị trí trên. Viết phương trình dao động của vật dưới dạng hàm số cosin.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
5 tháng 8 2021
Câu 64: Một vật dao động điều hoà trên trục x’0x với chu kỳ T = 0,5s, Gốc toạ độ O là vị trí cân bằng của vật. Lúc t = 0 vât đi qua vị trí có li độ x = 3 cm, và vận tốc bằng 0. Phương trình dao động của vật:
A. x = 5cos(4π.t)(cm) B. x = 5cos(4π .t +π)(cm)
C. x = 3cos(4π.t +π)(cm) D. x = 3cos(4π.t)(cm)
VT
25 tháng 12 2019
Chọn C
+ ω = 2π : T = 20 rad/s.
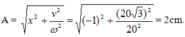
+ t = 0: x = 2cosφ = -1 =>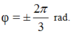 
v = -40 sinφ > 0 => sinφ < 0 => 
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.
VT
4 tháng 2 2017
Chọn A
+ Thay (x1 = 3cm; v1 = 8π cm/s) và (x2 = 4cm; v2 = 6π cm/s) vào 
ta được hệ phương trình hai ẩn A2 và 
. Giải hệ phương trình ta được A = 5cm và ω = 2π rad/s.
+ Tìm giá trị các đại lượng thay vào:
+ t = 0: vật qua vị trí cân bằng theo chiều dương => φ = - π/2 rad.
+ Thay số: x = 5cos(2πt - π/2)(cm).
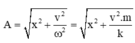
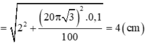
\(Acos\left(\omega t=\varphi\right)\)
\(v=-A\omega sin\left(\omega t+\varphi\right)\)
\(a=-A\omega^2cos\left(\omega t+\varphi\right)\)
t = 0
\(x=Acos\varphi=-\sqrt{2}\)
\(v=-A\omega sin\varphi=-\pi\sqrt{2}\)
\(a=-A\omega^2cos\varphi=\pi^2\sqrt{2}\)
Lấy a chia cho x ta được \(\omega=\frac{\pi rad}{s}\)
v chia cho a ta được \(tan\varphi=-1\) mà cos góc này nhỏ hơn 0 nên \(\varphi=\frac{3\pi}{4}\)
A=2cm
Vậy \(x=2cos\left(\pi t+\frac{3\pi}{4}\right)cm\)
s k có số