1 con lắc lò xo có khối lượng vật nhỏ là 50g. Con lắc dao động điều hòa theo 1 trục cố định nằm ngang với phương trình \(x=Acos\omega t\). Cứ sau những khoảng thời gian 0.05s thì động năng và thế năng của vật lại bằng nhau.Lấy \(\pi^2=10\). Lò xo của con lắc có độ cứng là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
15 tháng 4 2018
Đáp án A
Thế năng và động năng bằng nhau sau các khoảng thời gian Δt = 0,25T → T = 4Δt = 0,2 s
Độ cứng của lò xo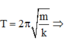 
k = 50N/m
VT
2 tháng 7 2019
Động năng và thế năng của vật lại bằng nhau sau các khoảng thời gian
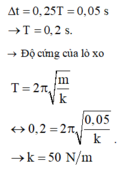
Đáp án A
VT
13 tháng 6 2017
Chọn A
+ Cứ sau khoảng thời gian T/4 thì động năng lại bằng thế năng
=> T/4 = 0,05 => T = 0,2s => ω = 10π rad/s.
+ Mà w= k m , thay m = 50g = 0,05kg và ω = 10π rad/s vào => k = 50 N/m.
VT
4 tháng 1 2019
Đáp án A
Động năng của vật bằng thế năng sau các khoảng thời gian t = 0,25T, vậy T = 0,2
→ Độ cứng của lò xo k = m ω 2 = m 2 π T 2 = 50 N/m
VT
9 tháng 5 2019
Đáp án A
+ Động năng và thế năng của vật lại bằng nhau sau các khoảng thời gian
Δ t = 0 , 25 T = 0 , 05 s → T = 0 , 2 s .
Độ cứng của lò xo T = 2 π m k ↔ 0 , 2 = 2 π 0 , 05 k → k = 50 N / m
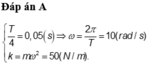
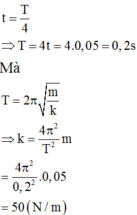
Vẽ vòng tròn ta ta có thể thấy được vị trí góc pha mà thế năng bằng động năng là
\(\varphi=\left(2k+1\right)\frac{\pi}{4}\)
Cứ sau góc \(\frac{\pi}{2}\) thì thế năng bằng động năng tương ứng với T/4
hu kỳ dao động là T = 0.2s suy ra \(\omega=10\pi\)
\(k=\omega^2m=\frac{50N}{m}\)