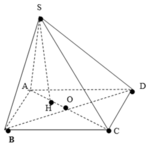
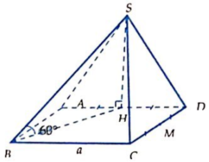
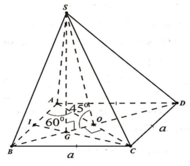
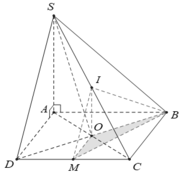
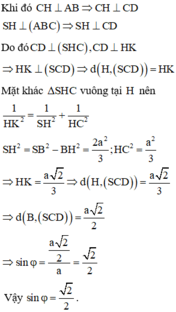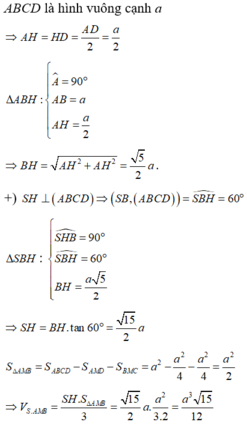Cho hình chóp S.ABCD có ABCD là hình thoi tâm O cạnh a, góc ABC = 60 độ. Hình chiếu vuông góc của S lên (ABCD) là trung điểm của OB, SC tạo với (ABCD) góc 60 độ. Gọi M là trung điểm CD. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AM và SB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BD
Bảo Duy Cute
14 tháng 8 2016
Đúng(0)
Những câu hỏi liên quan
18 tháng 12 2016
a) Dễ dàng chứng minh tam giác ABC và ACD đều
Suy ra AC=a, SA= AC.tan(gócSCA)=a.tan(600)
\(V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.a\sqrt{3}.a^2.\frac{\sqrt{3}}{2}=\frac{a^3}{2}\)
b) Có 2 cách làm để tìm khoảng cách từ H đến mp(SCD), nhưng bạn nên chọn phương pháp tọa độ hóa cho dễ
Chọn A làm gốc tọa độ , các tia AD, AI, AS lần lượt trùng tia Ax, Ay, Az
Có ngay tọa độ các điểm \(S\left(0;0;a\sqrt{3}\right)\) , \(D\left(a;0;0\right)\) , \(I\left(0;\frac{a\sqrt{3}}{2};0\right)\)
\(\Rightarrow C\left(\frac{a}{2};\frac{a\sqrt{3}}{2};0\right)\)
theo số liệu đã cho, dễ xác định được điểm H chia đoạn SI với tỷ lệ 2:1
\(\Rightarrow H\left(0;\frac{a}{\sqrt{3}};\frac{a}{\sqrt{3}}\right)\)
Bây giờ chỉ cần viết pt (SCD) là tính được ngay khoảng cách từ H đến SCD
\(\left(SCD\right):\sqrt{3}x+y+z-\sqrt{3}=0\)
\(d\left(H\text{/}\left(SCD\right)\right)=\frac{a\sqrt{3}}{\sqrt{5}}\)
DN
18 tháng 12 2016
Bạn ơi bạn chỉ mình cách bình thường được ko? Vì mình chưa học tọa độ hóa.
CM
5 tháng 8 2017
Đáp án D
Do B A D ⏜ = 120 o ⇒ A B C ⏜ = 60 o
⇒ A C = a ⇒ H C = 3 a 4
Ta có
Ta có S A B C D = 1 2 A C . B D = 1 2 a . a 3 = a 2 3 2
⇒ V S . A B C D = 1 3 S H . S A B C D = 3 a 3 8
CM
28 tháng 7 2019
Chọn B.
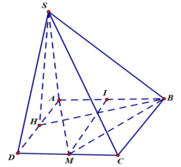
Kẻ MI vuông góc với AB 
Ta có: 
xét tam giác vuông SHB tại H ta có:
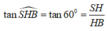
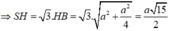
Vậy 
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 6 2021
Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(\Rightarrow\) CH là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCH}=60^0\)
Do \(\widehat{ABD}=60^0\Rightarrow\) các tam giác ABD và BCD là tam giác đều cạnh a
\(\Rightarrow\widehat{ABC}=120^0\)
Áp dụng định lý hàm cos cho tam giác BCH:
\(CH=\sqrt{BC^2+BH^2-2BC.BH.cos120^0}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow SH=CH.tan60^0=\dfrac{a\sqrt{21}}{2}\)
\(V=\dfrac{1}{3}SH.2S_{ABD}=\dfrac{1}{3}.\dfrac{a\sqrt{21}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{7}}{8}\)
CM
6 tháng 3 2019
Chọn đáp án A
Từ kẻ đường thẳng vuông góc với SC cắt SC tại K.
