Một vật có khối lượng m=250g treo vào lò xo có độ cứng k=25N\m. từ VTCB ta truyền cho vật một vận tốc 40cm\s theo phương của lò xo. chọn t=0 khi vật đi qua VTCB theo chiều âm. phương trình dao động của vật có dạng nào
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
8 tháng 6 2017
Chọn đáp án A
Δ l 0 = m g k = 2 , 5 c m ω = k m = 20 → A = x 2 + v 2 ω 2 A = l − Δ l 0 2 + v 2 ω 2 = 2 , 5 2 c m
VT
30 tháng 9 2017
Chọn đáp án B
Cách 1: Giải truyền thống
Biên độ dao động: A = x 2 + v 2 ω 2 = x 2 + v 2 m k = 3 2 + 30 2 .1 100 = 3 2 c m
Khi t = 0 → x = 3 → A = 3 2 x = A 2 v < 0 ⇒ φ = π 4 ⇒ 3 2 cos 10 t + π 4 c m
Cách 2: Dùng máy tính cầm tay
Cơ sở lí thuyết: x = A cos ω t + φ → t = 0 x ¯ = A cos φ + i sin φ (Biểu diễn phức).
Mặt khác: t = 0 → x = A cos φ v = − A ω sin φ ⇒ x ¯ = A cos φ + i sin φ = x − v ω i .
Bước 1: Bấm S H I F T M o d e 4 (Cài chế độ rad).
Bước 2: M o d e 2 S H I F T M o d e ∨ 3 2 (Cài chế độ tính toán).
Nhập biểu thức 3 − − 30 10 i màn hình xuất hiện.
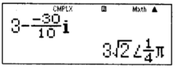
Chú ý: Do gốc tọa độ và chiều truyền vận tốc ta có x = 3 ; v < 0 . Các trường hợp khác thì dấu của x và v có thể thay đổi, bạn đọc cẩn thận chọn dấu cho phù hợp, tránh trường hợp chọn nhầm và nhập máy từ đó dẫn đến kết quả sai.
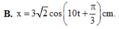
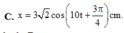
PT dao động tổng quát là: \(x=A\cos(\omega t + \varphi)\)
Ta lần lượt tìm \(\omega; A; \varphi\)
Tần số góc: \(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{25}{0,25}}=10(rad/s)\)
Vận tốc ở VTCB là vận tốc cực đại \(\Rightarrow v_{max}=\omega.A\Rightarrow A = \dfrac{40}{10}=4cm\)
Thời điểm ban đầu \(t=0\Rightarrow x_0=A\cos(\varphi)\Rightarrow \cos\varphi=0\)
Do \(v<0\Rightarrow \varphi>0\)
Suy ra \(\varphi=\dfrac{\pi}{2}\)
Vậy PT dao động: \(x=4\cos(10 t +\dfrac{\pi}{2}) (cm)\)
Nguyễn Thị Thảo Vân sướng nha dc thầy giải cho luôn