Cho hình bình hành ABCD và một điểm M tùy ý. Chứng minh rằng 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MH
2
Những câu hỏi liên quan
PT
1
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
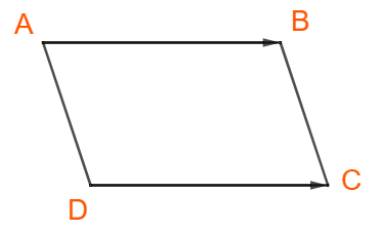
a) ABCD là hình bình hành nên \(\overrightarrow {DC} = \overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB} = \overrightarrow {BB} = \overrightarrow 0 \)
b) \(\overrightarrow {MA} + \overrightarrow {MC} = \left( {\overrightarrow {MB} + \overrightarrow {BA} } \right) + \left( {\overrightarrow {MD} + \overrightarrow {DC} } \right)\)
\(= \left( {\overrightarrow {MB} + \overrightarrow {MD} } \right) + \left( {\overrightarrow {BA} + \overrightarrow {DC}} \right)\)
\(= \overrightarrow {MB} + \overrightarrow {MD} \) (Vì \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0} \))
11 tháng 7 2023
1: Xét ΔADK và ΔCNK có
góc AKD=góc CKN
góc DAK=góc NCK
=>ΔADK đồng dạng với ΔCNK
2: Xét ΔKAM và ΔKCD có
góc KAM=góc KCD
góc AKM=góc CKD
=>ΔKAM đồng dạng với ΔKCD
=>KA/KC=KM/KD
=>KA*KD=KM*KC
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \)
\( \Leftrightarrow \overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {MO} + \overrightarrow {OB} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OD} = 4\overrightarrow {MO} \)
\( \Leftrightarrow 4\overrightarrow {MO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) = 4\overrightarrow {MO} \)
\( \Leftrightarrow 4\overrightarrow {MO} + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MO} \\ \Leftrightarrow 4\overrightarrow {MO} = 4\overrightarrow {MO} \) (luôn đúng)
(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)
b) ABCD là hình bình hành nên ta có \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Suy ra \(\)\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AC} = \overrightarrow {AC} + \overrightarrow {AC} = 2\overrightarrow {AC} \) (đpcm)
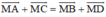
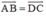
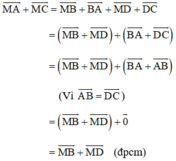
VT=\(\overrightarrow{MB}\)+\(\overrightarrow{BA}\)+\(\overrightarrow{MD}\)+\(\overrightarrow{DC}\)
=(\(\overrightarrow{MB}\)+\(\overrightarrow{MD}\))+(\(\overrightarrow{BA}\)+\(\overrightarrow{DC}\))
=\(\overrightarrow{MB}\)+\(\overrightarrow{MD}\)+\(\overrightarrow{0}\) (vì \(\overrightarrow{BA}\) và \(\overrightarrow{DC}\) đối nhau)
=\(\overrightarrow{MB}\)+\(\overrightarrow{MD}\)(đpcm)