Xem hình. Biết góc EOF = 35 độ, góc cEb= 70 độ, cho Oa // Eb.
a.Tính số đo các góc FOa ; góc bFd.\
b.chứng minh rằng Od là tia phân giác của góc cOa
O a E F c d b 35 độ 70 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì đường trung trực của `AC` cắt `AB` tại `D.`
`@` Theo tính chất của đường trung trực (điểm nằm trên đường trung trực của `1` đoạn thẳng thì cách `2` đầu mút đoạn thẳng đó)
`-> \text {DA = DC}`
Xét `\Delta ACD`: `\text {DA = DC}`
`-> \Delta ACD` cân tại `D.`
`-> \hat {A} = \hat {ACD}` `(1)`
Vì `\text {CD}` là tia phân giác của $\widehat {ACB} (g$$t)$
`->` $\widehat {ACD} = \widehat {BCD} =$ `1/2` $\widehat {ACB}$ `(2)`
Từ `(1)` và `(2)`
`->` $\widehat {ACB} = \widehat {2C_2} = \widehat {2A}$
Mà `\hat {A}=35^0`
`->` $\widehat {ACB}$`=35^0*2=70^0`
Xét `\Delta ABC`:
$\widehat {BAC} + \widehat {ABC}+ \widehat {ACB}=180^0 (\text {định lý tổng 3 góc trong 1 tam giác})$
`-> 35^0+` $\widehat {ABC} + 70^0=180^0$
`->` $\widehat {ABC}= 180^0-35^0-70^0=75^0$
Xét các đáp án trên `-> C (tm)`.

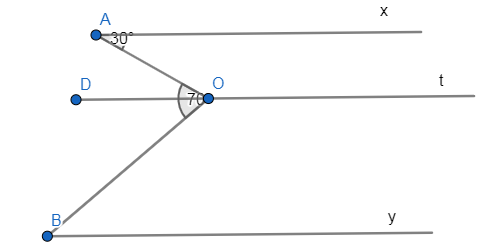
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:
\(\widehat{xAO}=\widehat{AOD}\) (So le trong)
\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)
Mà OD//By
\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)

Ta có :
AOB = 50 độ
BOM = 30 độ
mà AOB + BOM = AOM
=> 50 + 30 = 80 độ

a) số đo góc yOz là ;
góc xOz - góc xOy = 180 - 70 = 110o
b) số đo góc aOy là
70:2 = 35o
số đo góc zOa là
110+35 = 145o
c) số đo góc yOb là
110:2= 55o
số đo góc aob là
55 + 35 = 90o

Mấy bài này dễ mà, các bn cứ động não suy nghĩ ik là lm đk, chẳng lẽ thầy cô các cậu k dạy nhiều dạng toán hình kiểu này, ik thi mà gặp phải mấy bài này chắc tụi mik sung sướng tôt đỉnh quá
=? nha bạn