Một con lắc lò xo có khối lượng m được gắn vào một lò xo treo thẳng đứng có khối lượng ko đánh kể. Khi vật ở vtcb lò xo giản 4cm. Đưa vật đến vị trí lò xo nén 4cm rồi buông nhẹ. Tính thời gian lò xô bị nén trong 1chu kì. Lấy g= 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Biên độ: \(A=10cm\)
Tần số góc: \(\omega=10(rad/s)\)
Tại vị trí lò xo bị giãn \(5cm\) thì li độ của vật là: \(x=-10+5=-5cm\)
Vật đang đi lên là chuyển động theo chiều âm.
\(\Rightarrow \cos\varphi=-\dfrac{5}{10}=-0,5\)
\(\Rightarrow \varphi = \dfrac{2\pi}{3}\) (rad) (vì vật chuyển động theo chiều âm nên \(\varphi < 0\) )
PT dao động: \(x=10\cos(10t+\dfrac{2\pi}{3}) (cm)\)
Ở VTCB lò xo giãn 10 cm, như vậy để nó giãn 5cm thì từ VTCB phải đi lên 5cm.
Chiều dương hướng xuống, nên li độ lúc đó phải bằng -5cm.

a) Vị trí lực đàn hồi cân bằng với trọng lực:
kx0 = mg => x0 = 0,02 m = 2 cm.
b) Vận tốc của vật tại vị trí lực đàn hồi cân bằng với trọng lực:
1/2 . k(xo)2 = ½k(vcb)2 => |vcb| = 0,2√5 m/s = 20√5 (cm/s).
a. Ở vị trí cân bằng thì lực đàn hồi cân bằng với trọng lượng
\(\Rightarrow F_{đh}=P\Rightarrow k.\Delta l_0=mg\)
\(\Rightarrow \Delta l_0=\dfrac{mg}{k}=\dfrac{0,4.10}{200}=0,02m=2cm\)
b. Vị trí đó chính là vị trí cân bằng.
Chọn gốc thế năng ở vị trí cân bằng.
Thả vật ở vị trí lò xo không giãn \(\Rightarrow x_1=2cm\)
Áp dụng định luật bảo toàn cơ năng ta có:
\(\dfrac{1}{2}.k.x_1^2=\dfrac{1}{2}.m.v^2\)
\(\Rightarrow v = x_1.\sqrt{\dfrac{k}{m}}=2.\sqrt{\dfrac{200}{0,4}}==20\sqrt 5 (cm/s)\)

Đáp án A
Phương pháp: Áp dụng định luật bảo toàn cơ năng W = Wđ + Wt
Cách giải:
Ta có : 
Khi 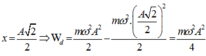

Độ dãn tỉ lệ với lực trác dụng lên nó.
\(\dfrac{P_1}{P_2}=\dfrac{\Delta l_1}{\Delta l_2}\Rightarrow\dfrac{10m}{10\cdot0,6}=\dfrac{4}{6}\)
\(\Rightarrow m=0,4kg\)
Chọn A

Ta có, tại vị trí cân bằng, lực đàn hồi của lò xo cân bằng với trọng lực của vật:
F d h = P ↔ k Δ l = m g → k = m g Δ l = 0 , 2.10 20 − 18 .10 − 2 = 100 N / m
Đáp án: C

Chọn C.
Tại vị trí cân bằng: Fđh = P ⟹ mg = k. ∆ l
Mặt khác ∆ l = 20 – 18 = 2 cm = 0,02 m.
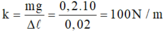

Đáp án A
Phương pháp: Áp dụng định luật bảo toàn cơ năng W = W đ + W t
Cách giải:
Ta có: W = W d + W t ⇒ W d = W − W t = m ω 2 A 2 2 − m ω 2 x 2 2
Khi x = A 2 2 ⇒ W d = m ω 2 A 2 2 − m ω 2 . A 2 2 2 2 = m ω 2 A 2 4
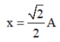
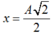
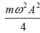
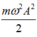
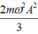
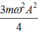
Ta có:\(\Delta\)l=4cm;A=8cm;T=2\(\pi\)\(\sqrt{\frac{\Delta l}{g}}\)=0,4(s)
2\(\alpha\)=\(\omega\)\(\Delta\)t nén
\(\Rightarrow\)\(\Delta\)t nén =\(\frac{2\alpha}{\omega}\)=\(\frac{2arccos\frac{\Delta l}{A}}{\frac{2\pi}{T}}\)=\(\frac{2.\frac{\pi}{3}}{2\pi}\).o,4=\(\frac{2}{15}\)(s)
Có j sai sót mong mn giúp đỡ
Bạn làm đúng rồi đó :)