Ông Bình định đi xe máy từ nhà tới cơ quan, nhưng xe không nổ được máy, nên đành đi bộ . Ở nhà con ông sửa được, liền lấy xe đèo ông đi tiếp . Nhờ đó tổng thời gian để ông đến được cơ quan chỉ bằng nửa thời gian nếu ông phải đi bộ suốt quãng đường nhưng gấp 3 lần nếu ông đi xe máy ngay từ nhà . Hỏi ông đi bộ được mấy phần quãng đường thì con ông đuổi kịp ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Gọi quãng đường từ nhà tới bưu điện là s.
Nếu đi bộ, Long sẽ mất 1 khoảng thời gian = S/5 (giờ).
Nếu đứng đợi và đi xe bus thì Long sẽ mất = 1/3 + s/30 (giờ)
Tức là nếu giả sử thời gian đi bộ = thời gian chờ + đi xe bus thì
s/5 = 1/3 + s/30
s/6 = 1/3
s = 2 (km).
Như vậy nếu quãng đường = 2 km, Long có thể đi bằng bất cứ cách nào cũng bằng nhau.
Còn nếu quãng đừng lớn hơn > 2 km, lúc đó cứ lấy đại 1 giá trị lớn hơn 2 (giả sử s = 30 km) thế vào 2 biểu thức trên.
Lúc đó, đi xe bus sẽ nhanh hơn.
Tương tự cho trường hợp quãng đường nhỏ hơn 2 km, đi bộ sẽ là giả pháp tốt hơn.

Đổi : 15p = 1/4h
1/4 h đi với vận tốc 40km/h đc quãng đường là:
40 . 1/4 = 10 (km)
Quãng đường còn lại là:
22 - 10 = 12 (km)
Vận tốc 10m/s ứng với vận tốc km/h là:
10 . 60 . 60 = 36000 (m) = 36km
Thời gian đi còn lại của chiếc mô tô là:
12 : 36 = 1/3h = 20p
Tổng thời gian mà chiếc mô tô đi là:
10 + 15 + 30 + 20 = 75 (phút)
Nếu bạn Tâm dùng xe đạp thì hết số phút là :
75 + 25 = 100p = 1h40p = 5/3 h
Vận tốc xe đạp là :
22 : 5/3 = 13,2 (km/h)

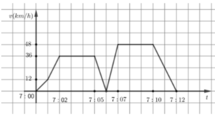
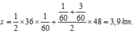
Có 12 phút bằng 0,2 giờ. Chọn gốc thời gian từ lúc 7h sang t = 0. Lúc ông A bắt đầu giảm tốc độ là 7h05 phút t = 5 60 Ta có quãng đường kể từ lúc giảm tốc đến lúc đến cơ quan là s = ∫ 5 60 12 60 v ( t ) d t chính là diện tích hình phẳng giới hạn bởi trục hoành; đường cong v(t) và hai đường thẳng t = 5 60 ; t = 12 60 . Diện tích hình phẳng trên được tính bằng cách chia nhỏ thành các hình đã biết có
 c
c
Chọn đáp án D.
*Chú ý các em có thể viết phương trình vận tốc xe ông A đi, tuy nhiên sẽ dài vì phải chia nhỏ v(t) theo từng khoảng thời gian.
Chọn đáp án D.


Gọi \(V_1;V_2\) lần lượt là vận tốc đi của người cha và người con.\(t_1;t_2;t';t_{dđ}\) lần lượt là thời gian đi xe của người cha, thời gian đi bộ của người con, thời gian về sớm hơn và thời gian dự đinh.
Ta có: \(S_{AC}+S_{CB}=S_{AB}\Rightarrow V_1.t_1+V_2.t_2=S_{AB}\Rightarrow15t_1+5t_2=S_{AB}\) (1)
Mà ta lại có: \(S_{AB}=15.t_{dđ}=15\left(t_1+\frac{1}{6}\right)=15t_1+2,5\left(2\right)\)
Từ (1) và (2) => \(5t_2=2,5\Rightarrow t_2=0,5\left(h\right)\)

`Answer:`
1)
Gọi số thời gian đi bộ là: `x(x<5)`
`=>` Thời gian đi xe đạp là: `5-x` giờ
`=>` Quãng đường người đấy đi xe đạp dài: `16.(5-x)(km)`
`=>` Quãng đường người đấy đi bộ dài: `5x(km)`
Vì tổng quãng đường đi được cả xe đạp và đi bộ là `58` ki-lô-mét nên ta có phương trình sau:
`16.(5-x)+5x=58`
`<=>80-16x+5x=58`
`<=>80-11x=58`
`<=>11x=22`
`<=>x=2`
Vậy thời gian đi bộ là `2` giờ và thời gian đi xe đạp là: `5-2=3` giờ.
2)
`15` phút `=1/4` giờ
Gọi vận tốc của người đấy là: `x(x>0)`
`=>` Thời gian dự định đến cơ quan của người đấy là: `9/x` giờ
`=>` Thời gian thực tế là: `3/x + 3/x + 9/x =15/x` giờ
Từ đây, ta có phương trình sau:
`<=>9/x + 1/4 =15/x`
`<=>9/x - 15/x = -1/4`
`<=>-6/x=-1/4`
`<=>x=24`
Gọi vận tốc của người đấy để đi kịp giờ là: `y(y>0)`
Thời gian để người đấy kịp giờ là: `9/24` giờ
`=>` Thời gian của người đấy sau khi thay đổi vận tốc là: `3/24 + 3/y + 9/y = 3/24 + 12/y` giờ
Từ đó, ta có phương trình sau:
`9/24 = 3/24 + 12/y`
`<=>-12/y= 3/24 - 9/24`
`<=>-12/y = -1/4`
`<=>y=48`
Vậy vận tốc người đấy cần đi để kịp giờ là \(48km/h\)