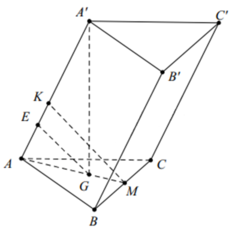
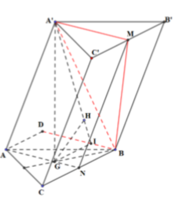
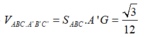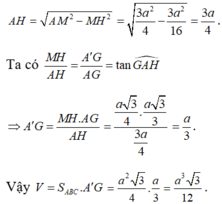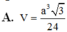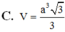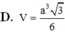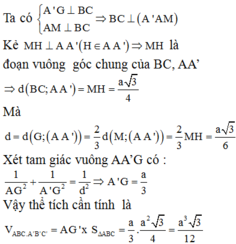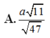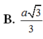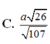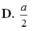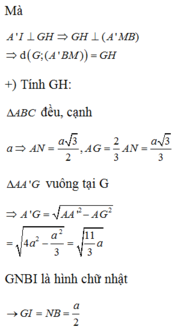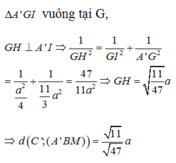Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu của A' lên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC. AA'=a, Gọi M, N là trung điểm BC, A'B. Tính khoảng cách từ điểm C đến mặt phẳng (AMN)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 7 2017
Chọn A.
Phương pháp:
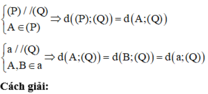
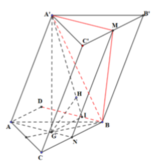
Gọi N là trung điểm của BC, G là trọng tâm tam giác ABC. Dựng hình chữ nhật ANBD
CM
15 tháng 8 2017
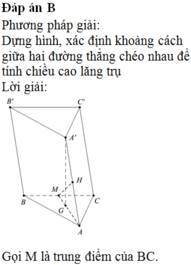
Chọn B.
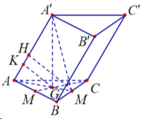
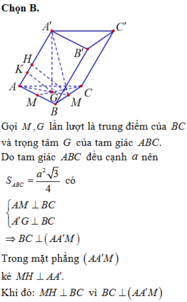
Gọi M,G lần lượt là trung điểm của BC và trọng tâm G của tam giác ABC.
Do tam giác ABC đều cạnh a nên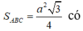 
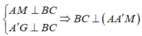
Trong mặt phẳng (AA'M) kẻ MH
⊥
AA'. Khi đó: 
Vậy MH là đoạn vuông góc chung của AA' và BC nên MH = a 3 4 .
Trong tam giác AA'G kẻ 
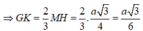
Xét tam giác AA'G vuông tại G ta có: 
Vậy thể tích của khối lăng trụ đã cho là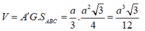 
CM
30 tháng 7 2017
Đáp án C
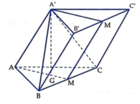
Ta dễ dàng chứng minh được AA'//(BCC'B')
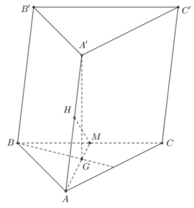
Gọi G là trọng tâm của tam giác ABC. Suy ra A'G ⊥ (ABC)
Ta có
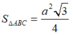
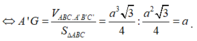
Lại có
Ta luôn có
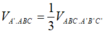
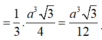
Gọi M, M' lần lượt là trung điểm của BC và B'C'. Ta có 
.
Mà MM'//BB' nên BC ⊥ BB' => BCC'B' là hình chữ nhật
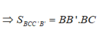
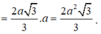
Từ:
CM
2 tháng 11 2019
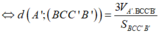
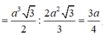
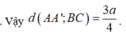
Đáp án D.
Gọi M là trung điểm BC, dựng 
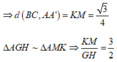
∆ AA'G vuông tại G, GH là đường cao => A'G = 1 3
Vậy 
