Bài 5.Cho tam giác ABC, kẻ các đường cao BD và CJ, Gọi H là trực tâm của tam giác , E làtrung điểm của AH, D là trung điểm của BC, CMR: I và J đối xứng với nhau qua ED
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2017
Cho tam giác nhọn ABC. Kẻ đường cao BI, CG. Gọi H là trực tâm của tam giác, E là trung điểm AH, D là trung điểm BC.CMR 2 điểm I và G đối xứng với nhau qua đường thẳng ED - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
SB
19 tháng 9 2017
Gọi F là giao điểm của AH và BC
CM AF vuông góc BC ko cần giải thích nha
ΔAIH vuông tại I có đường trung tuyên IE ứng với cạnh huyền AH
=> IE = IH = AE = \(\frac{AH}{2}\)(4)
=> ΔEIH cân tại E
=> \(\widehat{EIH}\) = \(\widehat{EHI}\)(1)
ΔIBC vuông tại I có trung tuyến ID ừng với cạnh huyền BC
=> ID = BD = DC = \(\frac{BC}{2}\)
=> ΔIDB cân tại D
=> \(\widehat{DBI}\) = \(\widehat{DIB}\) (2)
Cộng 1 và 2 VTV ta có
\(\widehat{EIH}\) + \(\widehat{DIB}\) = \(\widehat{EHI}\) + \(\widehat{DBI}\)
mà \(\widehat{EHI}\)= \(\widehat{BHF}\)(ĐỐI ĐỈNH)
=> \(\widehat{EIH}\) + \(\widehat{DIB}\) = \(\widehat{IBD}\) + \(\widehat{BHF}\)
=> \(\widehat{EIH}\) + \(\widehat{DIB}\) = 90
=> EI vuông góc ID
Tương tự ta có EG vuông góc DG
\(\Delta AHG\)có đường trung tuyên GE ứng với cạnh huyền AH
=> GE= AE= EH=\(\frac{AH}{2}\) (3)
Từ 3 và 4 => GE = EI
Xét \(\Delta EGD\)và \(\Delta EID\) CÓ
EG = EI (cmt)
ED cạnh chung
\(\widehat{EGI}\) = \(\widehat{EID}\) ( = 90)
=> \(\Delta EGD\)= \(\Delta EID\) ( CH-CGV)
=> \(\widehat{GED}\) = \(\widehat{EID}\)
\(\Delta EGI\)có ED là phân giác \(\widehat{GED}\)
đồng thời là đường trung tực của GI
=> G đối xứng với I qua ED
11 tháng 4 2022
Bài 1:
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường trung tuyến
Xét ΔABC có
AH là đường trung tuyến
BD là đường trung tuyến
AH cắt BD tại E
Do đó: E là trọng tâm của ΔABC
CM
4 tháng 10 2017
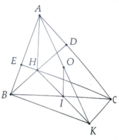
a, BHCK có I là trung điểm hai đường chéo
b, Ta có ∆ABK, ∆ACK vuông tại B và C nên A,B,K,C nằm trên đường tròn đường kính AK
c, Ta có OI là đường trung bình của ∆AHK => OI//AH
d, Gọi AH cắt BC tại M. Ta có BE.BA = BM.BC và CA.CD = CM.BC => ĐPCM
I là điểm nào thế bạn?
BÀI NÀY THẦY EM RA SAI ĐỀ Ạ