Lợi nhuận thu được khi bán x sản phẩm (\(0\le x\le10\)) tỉ lệ thuận với số sản phẩm bán được và khi số sản phẩm vượt qua 10 sản phẩm thì lợi nhuận tỉ lệ nghịch với số sản phẩm bán được. Biết rằng khi bán được 5 sản phẩm thì thu được lợi nhuận là 170 và hàm lợi nhuận là hàm liên tục. Hỏi lợi nhuận thu được đang giảm với tốc độ bao nhiêu ở mức sản phẩm 12?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giá nhập 1 sp là \(234000:130\%=180000\left(\text{đồng}\right)\)
Số tiền lời khi bán 1 sp là \(180000.30\%=54000\left(\text{đồng}\right)\)
Vậy cửa hàng nhập về \(13500000:54000=250\left(\text{sản phẩm}\right)\)

Số tiền dự kiến thu được là:
100*200000*130%=26000000(đồng)
Số tiền thực tế thu được là;
50*200000*130%+50*200000*80%=21000000 đồng
=>Số tiền thu về giảm 5000000 đồng so với dự kiến

a: Lợi nhuận thu về là: 20*5000-500=99500
b: Lợi nhuận là:
9000*8=72000(đồng)
Đặt 20n-500=72000
=>20n=72500
=>n=3625(sp)

Chọn A.
Gọi x; y lần lượt là số phẩm loại A; B.
Theo đề bài ta có: 2000x + 4000y = 40 000 hay x + 2y = 20
Suy ra: x = 20 - 2y.
Ta có ![]()
Xét hàm ![]()
Tập xác định D = (0; 10).
![]()
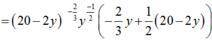
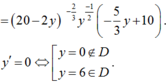
Nhận xét: ![]() nên dấu của y’ là dấu của biểu thức
nên dấu của y’ là dấu của biểu thức ![]()
Do đó hàm số đạt giá trị lớn nhất khi y = 6 và x = 8
Vậy ![]()

a) Thay x=100 ta được:
\(y = - {200.100^2} + 92000.100 - 8400000\)
\( = - 1200000\)
Thay x=200 ta được:
\(\begin{array}{l}y = - {200.200^2} + 92000.200 - 8400000\\ = 2000000\end{array}\)
Vậy với \(x = 100\) thì \(y = - 1200000\)
Với \(x = 200\) thì \(y = 2000000\)
b) Với mỗi giá trị của x có 1 giá trị tương ứng của y.

Áp dụng lợi nhuận = 170 thì không ra được ạ
Lời giải:
Theo như đề thì hàm lợi nhuận (y) và sản lượng (x) sẽ có dạng này:
Hàm lợi nhuận có dạng pt như sau:
$y=ax^2+bx+c$
Sản lượng bằng $0$ thì lợi nhuận đương nhiên bằng $0$
$\Rightarrow c=0$
ĐTHS đổi dấu tại $x=10$, tức là $x=10$ là điểm cực trị
$\Rightarrow \frac{b}{-2a}=10\Leftrightarrow b=-20a$
$y=ax^2-20ax$. Thay $x=5; y=170$ thì $a=-\frac{34}{15}$
Vậy hàm lợi nhuận là: $y=\frac{-34}{15}x^2+\frac{136}{3}x$
Tại $x=12$ thì $y=217,6$
Hàm lợi nhuận giảm với tốc độ là \(|y'(12).\frac{12}{217,6}|=0,5\) (%)
Vậy tại mức sản phẩm 12, khi mức sản phẩm tăng 1% thì lợi nhuận giảm 0,5 %.