ai giúp bài 5 với ạ ![]()

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5:
(d) vuông góc 2x-y-2018=0
=>(d): x+2y+c=0
(C): x^2+4x+4+y^2-6y+9-25=0
=>(x+2)^2+(y-3)^2=25
=>R=5; I(-2;3)
Theo đề, ta có: d(I;(d))=5
=>\(\dfrac{\left|1\cdot\left(-2\right)+2\cdot3+c\right|}{\sqrt{5}}=5\)
=>|c+4|=5căn 5
=>c=5căn5-4 hoặc c=-5căn 5-4

5:
d: \(A=\dfrac{9\left(x_1+x_2\right)+10-3m}{18\left(x_1x_2+2\right)^2+1}\)
\(=\dfrac{9\cdot\dfrac{m-2}{3}+10-3m}{18\cdot\left(\dfrac{m-6}{3}+2\right)^2+1}=\dfrac{3m-6+10-3m}{18\cdot\left(\dfrac{m-6+6}{3}\right)^2+1}\)
\(=\dfrac{4}{18\cdot\dfrac{m^2}{9}+1}=\dfrac{4}{2m^2+1}< =\dfrac{4}{1}=4\)
Dấu = xảy ra khi m=0

\(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}\)
=\(\dfrac{3}{1.4}+\dfrac{5}{4.9}+...+\dfrac{19}{81.100}\)
=\(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{9}+...+\dfrac{1}{81}-\dfrac{1}{100}\)
=\(1-\dfrac{1}{100}=\dfrac{99}{100}\)
Mà \(\dfrac{99}{100}< 1\) nên \(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}< 1\)

\(6x^2+xy-7x-2y^2+7y-5=-\left(y-2x-1\right)\left(2y+3x-5\right)\)
\(6x^2+xy-7x-2y^2+7y-5=-2y\left(y-2x-1\right)-3x\left(y-2x-1\right)+5\left(y-2x-1\right)=-\left(y-2x-1\right)\left(2y+3x-5\right)\)

Bài 5:
a: Xét ΔBEC và ΔADC có
\(\widehat{C}\) chung
\(\widehat{EBC}=\widehat{DAC}\)
Do đó: ΔBEC\(\sim\)ΔADC

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)

Bài 2:
a. $x^2=12y^2+1$ lẻ nên $x$ lẻ
Ta biết một scp khi chia 8 dư $0,1,4$. Mà $x$ lẻ nên $x^2$ chia $8$ dư $1$
$\Rightarrow 12y^2+1\equiv 1\pmod 8$
$\Rightarrow 12y^2\equiv 0\pmod 8$
$\Rightarrow y^2\equiv 0\pmod 2$
$\Rightarrow y$ chẵn. Mà $y$ nguyên tố nên $y=2$.
Khi đó: $x^2=12y^2+1=12.2^2+1=49\Rightarrow x=7$ (tm)
Bài 2:
b.
$x^2=8y+1$ nên $x$ lẻ. Đặt $x=2k+1$ với $k$ tự nhiên.
Khi đó: $8y+1=x^2=(2k+1)^2=4k^2+4k+1$
$\Rightarrow 2y=k(k+1)$
Vì $(k,k+1)=1, k< k+1$ và $y$ nguyên tố nên xảy ra các TH sau:
TH1: $k=2, k+1=y\Rightarrow y=3\Rightarrow x=5$ (tm)
TH2: $k=1, k+1=2y\Rightarrow y=1$ (vô lý)
TH3: $k=y, k+1=2\Rightarrow y=1$ (vô lý)
Vậy $(x,y)=(5,3)$ là đáp án duy nhất thỏa mãn.


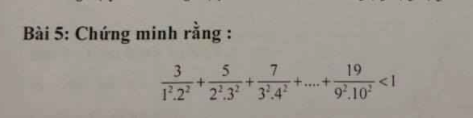 đang cần gấp bài 5 ai giúp mình với ạ :))
đang cần gấp bài 5 ai giúp mình với ạ :))


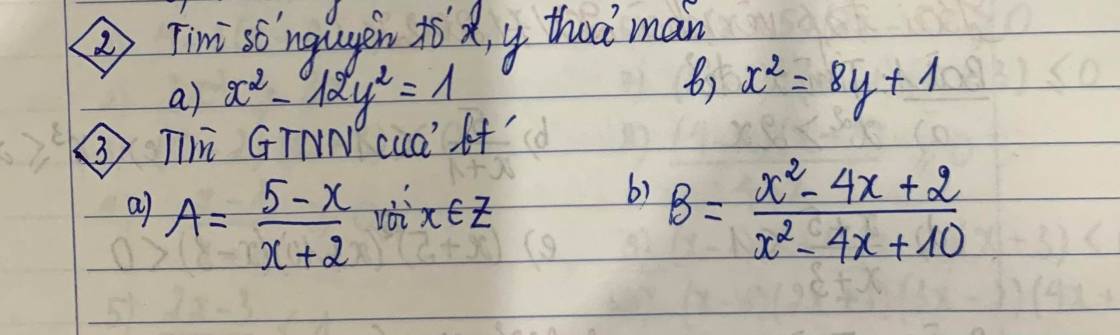
ta có:
khi khóa k ngắt:
R2 nt R3
Uv=U3=6V
\(\Rightarrow I_3=\frac{U_3}{R_3}=1.2A\)
mà I3=I2 nên I2=1.2A
U=U2+U3
\(\Leftrightarrow U=I_2R_2+I_3R_3=1.2R_2+6\left(1\right)\)
khi khóa k đóng
R3 nt (R1//R2)
Uv=U3=8V
\(\Rightarrow I_3=\frac{U_3}{R_3}=1.6A\)
\(\Rightarrow I_1+I_2=1.6A\)
\(\Leftrightarrow\frac{U_1}{R_1}+\frac{U_2}{R_2}=1.6\)
\(\Leftrightarrow\frac{U_1}{10}+\frac{U_2}{R_2}=1.6\)
mà U1=U2 nên:
\(\frac{U_1}{10}+\frac{U_1}{R_2}=1.6\)
\(\Leftrightarrow\frac{U_1R_2+10U_1}{10R_2}=1.6\)
\(\Leftrightarrow U_1\left(R_2+10\right)=16R_2\)
\(\Rightarrow U_1=\frac{16R_2}{R_2+10}\left(2\right)\)
ta lại có:
U=U3+U1
\(\Leftrightarrow U=8+U_1\)
thế (2) vào phương trình trên ta có:
\(U=8+\frac{16R_2}{R_2+10}\)
\(\Leftrightarrow U=\frac{8R_2+80+16R_2}{R_2+10}\)
\(\Leftrightarrow U=\frac{24R_2+80}{R_2+10}\left(3\right)\)
do U không đổi nên ta có:
(1)=(3)
\(\Leftrightarrow1.2R_2+6=\frac{24R_2+80}{R_2+10}\)
\(\Leftrightarrow\left(1.2R_2+6\right)\left(R_2+10\right)=24R_2+80\)
\(\Leftrightarrow1.2R^2_2+6R_2+12R_2+60=24R_2+80\)
\(\Leftrightarrow1.2R^2_2-6R_2-20=0\)
giải phương trình ta có:
R2=7.3Ω (loại R2=-2.3Ω do âm)
\(\Rightarrow U=14.76V\)