trên mặt nằm ngang không ma sát, một lò xo nhẹ có độ cứng k=100N/m một đầu cố định, đầu kia gắn
với vật nhỏ khối lượng m1= 100g.
Đặt vật m2 = 500g đứng yên tại vị trí lò xo không biến dạng, đưa vật m1 đến vị trí lò xo nén 10 cm rồi thả nhẹ
Coi va chạm của m1 và m2 là hoàn toàn đàn hồi. Khoảng cách gần nhất giữa hai vật khi hai vật chuyển động
cùng chiều sau khi va chạm gần giá trị nào nhất
A. 14cm B. 7,3 cm C. 8,2 cm D. 4 cm
đáp án C
thầy giúp em bài này với ạ. thầy giải thích giúp em phần in đậm luôn ạ em vẫn chưa hiểu rõ lắm (tức là làm sao để biết
vị trí gần nhất đấy thì m1 đang ở li độ nào ạ)
em cảm ơn thầy.

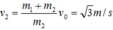
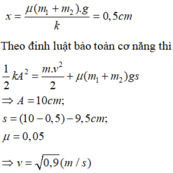
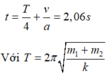







Va chạm đàn hồi không thi đâu bạn, không nên quan tâm về nó.
Gọi v1, v2 là vận tốc của vật m1, m2 sau va chạm, áp dụng CT tính vận tốc trong va chạm đàn hồi ta có:
\(\Rightarrow v_2 = \frac{2m_1.v_{max}}{m_1 + m_2} = \frac{2.0,1.0,1. \sqrt{\frac{100}{0,1}}}{0,1 + 0,5} = \frac{10\sqrt{10}}{30} = \frac{\sqrt{10}}{3}\) (m/s)
và
\( v_1 = \frac{m_1.v_{max} - v_2.m_2}{m_1} = A\omega - \frac{\sqrt{10}}{3}.5 = -\frac{2\sqrt{10}}{3}\) (m/s), \(v_1 <0\) nên vật m1 chuyển động theo chiều ngược lại.
Biên độ mới của vật m1 là A mới = \(\frac{v_1}{\omega } = \frac{\frac{2\sqrt{10}}{3}}{10\sqrt{10}} = \frac{2}{30} \)(m) = \(\dfrac{20}{3}\) (cm)
Sau T/4 thì 2 vật mới chuyển động cùng chiều ⇒ Quãng đường S m2 đi được là \(S = v_2.T/4 = \frac{\sqrt{10}}{3}.\frac{T}{4} = \frac{\sqrt{10}}{60}\) (m)
Khoảng cách = A mới + S = \(\frac{2}{30} + \frac{\sqrt{10}}{60} = 11,94\) (cm)
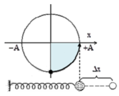
Còn khoảng cách gần nhất được tính như sau:
\(x_{m1} = A. cos(10 \pi t - \pi) = \frac{2}{30} cos(10 \pi t - \pi)\)
\(x_{m2} = v_2t = \frac{\sqrt{30}}{3}t\)
⇒ Khoảng cách = \(\left | x_{M2} - x_{M1} \right | = \frac{\sqrt{10}}{3}t - \frac{22}{30}cos(100 \pi t - \pi)\)
Khi vật m1 tới vị trí có khoảng cách gần m2 nhất thì tốc độ của m1 bằng tốc độ m2,
\(\Rightarrow x = \frac{A\sqrt{3}}{2}\) ⇒ sau thời gian là T/2 + T/6 ⇒quãng đường vật m2 đi được là
\(s_2 = v_2.t = \frac{\sqrt{10}}{3} . \frac{2T}{3} = 14,05\) cm.
⇒ Khoảng cách = \(14,05 - x = 14,05 - \frac{10}{\sqrt{3}} = 8,2 \) cm
⇒ Chọn đáp án C.