Biết O và O' là 2 nguồn nước cùng biên độ, tần số nhưng ngược pha nhau và cách nhau 4 cm.Chọn trục tọa độ Ox nằm trên mặt nước và vuông góc với đoạn OO' thì điểm không dao động trên trục Ox có tọa độ lớn nhất là 4,2 cm. Tìm số điểm dao động cực đại trên trục Ox
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
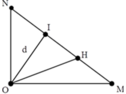
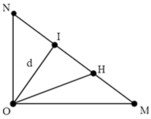
+ Gọi I là một điểm bất kì nằm trên MN
Độ lệch pha dao động giữa nguồn và I là: ∆ φ = 2 π d λ = ( 2 k + 1 ) π ⇒ d = ( 2 k + 1 ) λ 2
+ Gọi H là trung điểm của MN, khi đó dựa vào tính chất của tam giác vuông ta có O H = M N 2 = 2 13 λ
+ Số điểm dao động ngược pha với O trên đoạn NH:
2 13 λ ≤ ( 2 k + 1 ) λ 2 ≤ 12 λ ⇒ 6 , 7 ≤ k ≤ 12 , 5 → Có 5 điểm.
+ Số điểm dao động ngược pha với O trên đoạn MH: 2 13 λ ≤ ( 2 k + 1 ) λ 2 ≤ 8 λ ⇒ 6 , 7 ≤ k ≤ 7 , 5 → Có 1 điểm.
Vậy có tất cả 6 điểm dao động ngược pha với O trên đoạn MN.

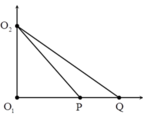
+ Vì Q dao động với biên độ cực đại nên: QO2 - QO1 = kl
+ Vì giữa P và Q còn có 1 cực đại và P dao động với biên độ cực tiểu nên:

® OM » 3,1 cm
® MP » 1,4 cm
Đáp án A

Vì Q dao động với biên độ cực đại nên: QO2 - QO1 = kλ
- Vì giữa P và Q còn có 1 cực đại và P dao động với biên độ cực tiểu nên:
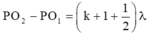
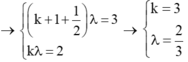
- Điểm M gần P nhất nên sẽ ứng với k = 5
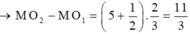
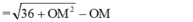
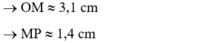

Đáp án A
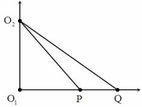
+ Vì Q dao động với biên độ cực đại nên: Q O 2 - Q O 1 = kl
+ Vì giữa P và Q còn có 1 cực đại và P dao động với biên độ cực tiểu nên:
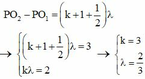
+ Điểm M gần P nhất nên sẽ ứng với k = 5
® M O 2 - M O 1
![]()
![]()
® OM » 3,1 cm
® MP » 1,4 cm

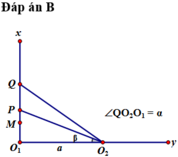
Có tan P O 2 Q = tan α - β = tan α - tan β 1 + tan α . tan β = 8 a - 4 ٫ 5 a 1 + 8 a . 4 ٫ 5 a = 3 ٫ 5 a + 36 a
Áp dụng BĐT Cauchy cho mẫu, ta tìm được
tan P O 2 Q ≤ 3 ٫ 5 12 ⇒ P O 2 Q m a x ⇔ a = 6 c m .
Q là cực đại, P là cực tiểu gần nguồn hơn và gần Q nhất nên ta có :
Q O 2 - Q O 1 = k λ P O 2 - P O 1 = k + 0 ٫ 5 λ ⇔ k λ = 2 k + 0 ٫ 5 λ = 3 ⇔ λ = 2 c m k = 1
Gọi M là cực đại gần P nhất. Vì Q là cực đại với k = 1 nên M là cực đại với k = 2.
⇒ M O 2 - M O 1 = 2 λ = 4 ⇒ M O 1 2 + 36 - M O 1 = 4 ⇔ M O 1 = 2 ٫ 5 c m
Suy ra PM = 4,5 – 2,5 = 2 (cm).


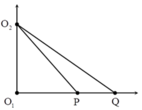

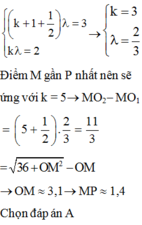

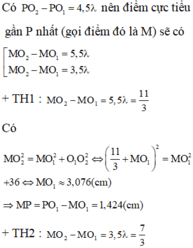

Điểm M có tọa độ 4,2 cm nên \(O'M=\sqrt{OM^2+O'O^2}=5,8cm\)
Do M dao động với biên độ cực tiểu và xa nguồn nhất nên
\(O'M-OM=\text{λ}\)
\(\Rightarrow\text{λ}=1,6cm\)
Từ đó tính được có 4 điểm dao động cực đại trên đoạn OO' nên có 2 điểm dao động cực đại trên đoạn ON (với N là trung điểm OO')
Mỗi đường hypebol qua điểm dao động cực đại trên đoạn ON cắt trục Ox tại 2 điểm
Vậy có 4 điểm dao động với biên độ cực đại trên Ox