x^2+y^2-4x+6y-3=0 viết pt ảnh qua phép đối xứng tâm I(-2,3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2021
Phương trình đường tròn (C) : (x + 1)2 + (y - 3)2 = 2 + 1 + 9 = 12
Vậy (C) có tâm A(-1 ; 3) và bán kính R = \(2\sqrt{3}\)
a, Phép đối xứng qua tâm O biết (C) thành một đường tròn có tâm có tọa độ là (1 ; -3) và bán kính vẫn bằng \(2\sqrt{3}\)
Phương trình đường tròn đó là : (x - 1)2 + (y + 3)2 = 12
b, Đối xứng qua tâm I (2 ; -3) biến A thành B và I là trung điểm của AB và bán kính đường tròn mới vẫn bằng \(2\sqrt{3}\). TÌm tọa độ I là được
DN
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 10 2020
Đường tròn (C) tâm \(I\left(2;-3\right)\) bán kính \(R=4\)
(C') là ảnh của (C) qua phép đối xứng trục Oy có tâm \(I'\left(-2;-3\right)\) và cùng bán kính với (C)
Phương trình (C'):
\(\left(x+2\right)^2+\left(y+3\right)^2=16\)
Bạn tự khai triển ra nếu muốn
CM
9 tháng 6 2018
a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2 + y 2 − 2 x + 6 y + 6 = 0 .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0.
Lấy một điểm trên d, chẳng hạn N(0; 9).
Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).
Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),
bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).
Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x − 3 2 + y − 1 2 = 4 .
CM
21 tháng 6 2018
a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.
b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.
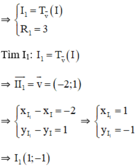
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.
c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox
⇒ R2 = 3 và I2 = ĐOx(I)
Tìm I2: I2 = ĐOx(I) ⇒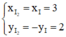 
⇒ I2(3; 2)
⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.
d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.
⇒ R3 = 3 và I3 = ĐO(I)
Tìm I3: I3 = ĐO(I) ⇒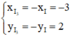 
⇒ Phương trình đường tròn cần tìm: (x + 3)2 +(y – 2)2 = 9.
CM
17 tháng 2 2019
Dùng công thức tọa độ của phép đối xứng tâm I(−2;1), ta có: M ′ = D 1 ( M )
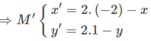
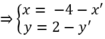
Thế (x;y) vào phương trình d, ta có phương trình:
d′: 2(−4 − x′) − (2 − y′) + 6 = 0
⇒ d′: 2x′ − y′ + 4 = 0.
Đổi kí hiệu, ta có phương trình: d′: 2x – y + 4 = 0
\(x^2+y^2-4x+6y-3=0\Leftrightarrow\left(x-2\right)^2+\left(y+3\right)^2=16\)
Đường tròn (C) tâm \(A\left(2;-3\right)\) bán kính \(R=4\)
Gọi (C') là ảnh của (C) qua phép đối xứng tâm I \(\Rightarrow\) (C') có tâm B là ảnh của A qua phép đối xứng tâm I và bán kính \(R'=R=4\)
\(\left\{{}\begin{matrix}x_B=2x_I-x_A=-6\\y_B=2y_I-y_A=9\end{matrix}\right.\) \(\Rightarrow B\left(-6;9\right)\)
Phương trình (C'):
\(\left(x+6\right)^2+\left(y-9\right)^2=16\)