đoạn mạch AB gồm R = 50 ôm cuộn dây có độ tụ cảm L = 0,4/pi H và điện trở r = 60 ôm tụ điện có điện dung C thay đổi và mắc theo thứ tự trên. đặt vào hai đầu mạch một điện áp xoay chiều có dạng 220 căn 2 cos 100pit người ta thấy rằng khi C = Cm thì điện áp hiệu dụng ở hai đầu đoạn mạch chứa cuộn dây và tụ điện đạt cực tiểu Umin. giá trị cua Cm và Umin lần lượt là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A
Đặt điện áp giữa hai đầu đoạn mạch chứa cuộn dây và tụ điện là U
Ta có:
U = I r 2 + ( Z L - Z C ) 2 = U A B ( R + r ) 2 + ( Z L - Z C ) 2 r 2 + ( Z L - Z C ) 2
U = U A B ( R + r ) 2 + ( Z L - Z C ) 2 r 2 + ( Z L - Z C ) 2 = U A B 1 + R 2 + 2 R r r 2 + ( Z L - Z C ) 2
=> U = Umin khi ZC = ZCmin = ZL = 40Ω => Cmin = 10 - 3 4 π F
U = Umin = U A B ( R + r ) 2 r 2 = U A B r R + r = 120V

Đáp án D
+ Điện áp hiệu dụng giữa hai đầu đoạn mạch chứa cuộn dây và tụ điện:
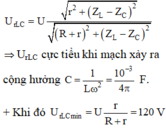

Đáp án D
Điện áp hai đầu đoạn mạch chứa tụ điện và cuộn dây được xác định bởi biểu thức
U r L C = U r 2 + Z L − Z C 2 R + r 2 + Z L − Z C 2 = U 1 + R 2 + 2 R r r 2 + Z L − Z C 2 → U r L C min khi mạch xảy ra cộng hưởng Z L = Z C
→ U r L C min = U 1 + R 2 + 2 R r r 2 → 20 = 100 1 + R 2 + 2 R .10 10 2 → R = 40 Ω

+ \(U_{AM}=I.Z_{AM}\), \(Z_{AM}\)không thay đổi, nên để \(U_{AM}\) đạt giá trị lớn nhất khi thay đổi C thì dòng điện Imax --> Xảy ra hiện tượng cộng hưởng: \(Z_L=Z_C\)
và \(I=\frac{U}{R+r}\)
Công suất của cuộn dây khi đó: \(P=I^2.r=\left(\frac{U}{R+r}\right)^2.r\) (*)
+ Nếu đặt vào 2 đầu AB một điện áp không đổi và nối tắt tụ C thì mạch chỉ gồm r nối tiếp với R (L không có tác dụng gì)
Cường độ dòng điện của mạch: \(I=\frac{25}{R+r}=0,5\Rightarrow R+r=50\)
Mà R = 40 suy ra r = 10.
Thay vào (*) ta đc \(P=\left(\frac{200}{50}\right)^2.10=160W\)
Bạn học đến điện xoay chiều rồi à. Học nhanh vậy, mình vẫn đang ở dao động cơ :(

Đáp án A
+ Để điện áp hai đầu cuôn dây dẫn cực đại thì mạch xảy ra cộng hưởng
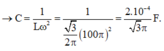

Đáp án C
+ Cảm kháng và dung kháng của mạch Z L = 100 Ω , Z C = 400 Ω
Ta có
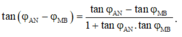
Khi u A N vuông pha với u M B ta có
![]()

Ta có: $U_{Lr-C}= U \dfrac{\sqrt{r^2 + (Z_L-Z_C)^2}}{\sqrt{(R+r)^2 + (Z_L-Z_C)^2}}.$
Do đó, theo tính chất hàm số:
$f(Z_C)=\dfrac{r^2 + (Z_L-Z_C)^2}{(R+r)^2 + (Z_L-Z_C)^2}.$
Ta có hàm số đạt cực tiểu khi $Z_C=Z_L.$
Ta tìm được:
$C=\dfrac{10^{-3}}{4 \pi} F.$
Thay vào biểu thức trên ta được:
$U_{min}=120.$