câu 1 : Gọi t là khoảng thời gian để số hạt nhân nguyên tử của một chất phóng xạ giảm đi e lần (e=2,718 ) . Sau thời gian t=0,51t, số hạt nhân của chất phóng xạ đó còn lại bao nhiêu phần trăm ?
câu 2 : Một vật có khối lương M=300g, được treo vào một lò xo có độ cứng 100N/m . Khi M đang đứng yên thì vật m=200g bay theo phương thẳng đứng từ dưới lên với tốc độ 1m/s . tới va chạm vào M, sau va chạm hai vật dính vào nhau và cùng dao động điều hòa thèo phương thẳng đứng . Biên độ dao động và động năng cực đại của hệ lần lượt là :

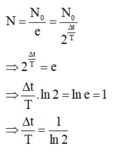
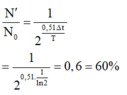
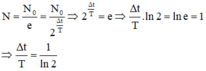
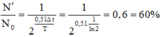

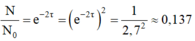

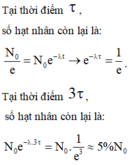

câu 1: Theo bài, sau Δt thì số hạt nhân giảm e lần, tức là \(\frac{No}{N}=e< =>e^{y\text{Δ}t}=e->Y\text{Δ}t=1\)
Tỉ lệ số hạt nhân còn lại so với ban đầu là \(\frac{No}{N}=\frac{N_0e-y\text{Δ}t}{No}=e^{-y\text{Δ}t}=e^{-0,51y\text{Δ}t}=e^{-0,51}=0,6=60\%\)
Bạn lưu ý: Mỗi câu hỏi chỉ hỏi 1 bài toán thôi nhé.
Câu 1: Câu hỏi của trương quang kiet - Học và thi online với HOC24
Câu 2:
Ta có va chạm mềm xảy ra(vì sau va chạm hai vật dính vào nhau).
Theo bảo toàn động lượng:
\(m.v_o =(M+m).v\)
Với v là vận tốc của hệ hai vật sau va chạm.
Tính ra: \(v=40 cm/s\)
Sau va chạm, hệ dao động với tần số góc: \(\omega = \sqrt{\dfrac{k}{M+m}}=10\sqrt 2(rad/s)\)
Ban đầu chỉ có vật M lò xo dãn:
\(\Delta l=\dfrac{Mg}{k}\)
Sau khi có thêm vật m lò xo dãn:\(\Delta l'=\dfrac{(M+m)g}{k}\)
Lượng giãn thêm chính là độ lệch của vật so với vị trí cân bằng cũ, gọi là x
\(x=\Delta l'-\Delta l=\dfrac{m_0g}{k}=0,02m=2cm\)
.\(\Rightarrow A^2=x^2+\left(\dfrac{v}{\omega}\right)^2=2^2+(\dfrac{40}{10\sqrt 2})^2\)
\(\Rightarrow A = 2\sqrt 3cm\)
Tìm động năng cực đại chính là cơ năng của hệ: \(W=\dfrac{1}{2}kA^2=\dfrac{1}{2}.100.(0,02\sqrt3)^2=0,06(J)\)