Tính các giới hạn sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\lim\limits\left(\dfrac{1}{n^2}\right)=0\)
b: \(lim\left(-\dfrac{3}{4}\right)^n=0\)

a) \(\lim \frac{{8{n^2} + n}}{{{n^2}}} = \lim \left( {8 + \frac{1}{n}} \right) = \lim 8 + \lim \frac{1}{n} = 8 + 0 = 8\)
b) \(\lim \frac{{\sqrt {4 + {n^2}} }}{n} = \lim \frac{{n\sqrt {\frac{4}{{{n^2}}} + 1} }}{n} = \sqrt {\lim \left( {\frac{4}{{{n^2}}} + 1} \right)} = \sqrt {0 + 1} = 1\)

Câu a.
\(^{lim}_{x\rightarrow3}\dfrac{\sqrt{x+1}-x+1}{x^2-5x+6}\)
Nhân liên hợp ta đc:
\(^{lim}_{x\rightarrow3}\dfrac{x+1-\left(x-1\right)^2}{(x^2-5x+6)\cdot\left(\sqrt{x+1}+x-1\right)}\)
\(=^{lim}_{x\rightarrow3}\dfrac{-x^2+3x}{\left(x-3\right)\left(x-2\right)\left(\sqrt{x+1}+x-1\right)}\)
\(=^{lim}_{x\rightarrow3}\dfrac{-x}{\left(x-2\right)\cdot\left(\sqrt{x+1}+x-1\right)}\)
\(=\dfrac{-3}{\left(3-2\right)\cdot\left(\sqrt{3+1}+3-1\right)}=-\dfrac{3}{4}\)
Câu b.
\(^{lim}_{x\rightarrow-2}\left|x^3-3x\right|\)
\(=\left|\left(-2\right)^3-3\cdot\left(-2\right)\right|=\left|-2\right|=2\)
Câu này đơn giản chỉ thay số thôi nhé, nó ở dạng đa thức nữa!

a) Đặt \(f\left( x \right) = 2{x^2} - x\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to 3\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \left( {2x_n^2 - {x_n}} \right) = 2.\lim x_n^2 - \lim {x_n} = {2.3^2} - 3 = 15\).
Vậy \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right) = 15\).
b) Đặt \(f\left( x \right) = \frac{{{x^2} + 2x + 1}}{{x + 1}}\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to - 1\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \frac{{x_n^2 + 2{x_n} + 1}}{{{x_n} + 1}} = \lim \frac{{{{\left( {{x_n} + 1} \right)}^2}}}{{{x_n} + 1}} = \lim \left( {{x_n} + 1} \right) = \lim {x_n} + 1 = - 1 + 1 = 0\).
Vậy \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}} = 0\).

a) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{6x + 8}}{{5x - 2}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {6 + \frac{8}{x}} \right)}}{{x\left( {5 - \frac{2}{x}} \right)}} = \frac{6}{5}\)
b) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{6x + 8}}{{5x - 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {6 + \frac{8}{x}} \right)}}{{x\left( {5 - \frac{2}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{6 + \frac{8}{x}}}{{5 - \frac{2}{x}}} = \frac{6}{5}\).
c) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {9{x^2} - x + 1} }}{{3x - 2}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {9 - \frac{1}{x} + \frac{1}{{{x^2}}}} }}{{x\left( {3 - \frac{2}{x}} \right)}} = - \frac{3}{3} = - 1\).
d) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {9{x^2} - x + 1} }}{{3x - 2}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\sqrt {9 - \frac{1}{x} + \frac{1}{{{x^2}}}} }}{{x\left( {3 - \frac{2}{x}} \right)}} = \frac{3}{3} = 1\).
e) \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{{3{x^2} + 4}}{{2x + 4}} = - \infty \)
Do \(\mathop {\lim }\limits_{x \to - {2^ - }} \left( {3{x^2} + 1} \right) = 3.{\left( { - 2} \right)^2} + 1 = 13 > 0\) và \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{1}{{2x + 4}} = - \infty \)
g) \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{3{x^2} + 4}}{{2x + 4}} = + \infty \).
Do \(\mathop {\lim }\limits_{x \to - {2^ + }} \left( {3{x^2} + 1} \right) = 3.{\left( { - 2} \right)^2} + 1 = 13 > 0\) và \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{1}{{2x + 4}} = + \infty \)

a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{9x + 1}}{{3x - 4}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {9 + \frac{1}{x}} \right)}}{{x\left( {3 - \frac{4}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{9 + \frac{1}{x}}}{{3 - \frac{4}{x}}} = \frac{{9 + 0}}{{3 - 0}} = 3\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{7x - 11}}{{2x + 3}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {7 - \frac{{11}}{x}} \right)}}{{x\left( {2 + \frac{3}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{7 - \frac{{11}}{x}}}{{2 + \frac{3}{x}}} = \frac{{7 - 0}}{{2 + 0}} = \frac{7}{2}\)
c) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\sqrt {1 + \frac{1}{{{x^2}}}} }}{x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 + \frac{1}{{{x^2}}}} = \sqrt {1 + 0} = 1\)
d) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 1} }}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {1 + \frac{1}{{{x^2}}}} }}{x} = \mathop {\lim }\limits_{x \to - \infty } - \sqrt {1 + \frac{1}{{{x^2}}}} = - \sqrt {1 + 0} = - 1\)
e) Ta có: \(\left\{ \begin{array}{l}1 > 0\\x - 6 < 0,x \to {6^ - }\end{array} \right.\)
Do đó, \(\mathop {\lim }\limits_{x \to {6^ - }} \frac{1}{{x - 6}} = - \infty \)
g) Ta có: \(\left\{ \begin{array}{l}1 > 0\\x + 7 > 0,x \to {7^ + }\end{array} \right.\)
Do đó, \(\mathop {\lim }\limits_{x \to {7^ + }} \frac{1}{{x - 7}} = + \infty \)

Câu 1: Chọn câu đúng trong các câu sau:
A. Giới hạn đo của thước là khoảng cách giữa 2 vạch dài nhất liên tiếp của thước.
B. Giới hạn đo của thước là độ dài lớn nhất được ghi trên thước.
C. Giới hạn đo của thước là chiều dài lớn nhất của vật mà thước có thể đo được
D. Cả B và C đều đúng.
Câu 2: Chọn câu đúng trong các câu sau:
A. Độ chia nhỏ nhất của thước là độ dài giữa 2 vạch chia liên tiếp trên thước.
B. Độ chia nhỏ nhất là chiều dài nhỏ nhất của vật mà thước có thể đo được
C. Độ chia nhỏ nhất của thước là 1 mm.
D. Độ chia nhỏ nhất của thước là khoảng cách giữa 2 vạch có in số liên tiếp trên thước.
Câu 3: Để đo kích thước (dài, rộng, dày) của cuốn sách Vật Lý 6, ta dùng thước nào là hợp lý nhất trong các thước sau:
A. Thước có giới hạn đo 1m và độ chia nhỏ nhất 1cm.
B. Thước có giới hạn đo 50cm và độ chia nhỏ nhất là 1cm.
C. Thước có giới hạn đo 20cm và độ chia nhỏ nhất 1mm
Câu 4: Để đo chiều dài vải, người bán hàng phải sử dụng thước nào sau đây là hợp lý
| A. Thước cuộn | B. Thước kẻ |
| C. Thước thẳng (thước mét) | D. Thước kẹp |
Câu 5: Trên thước thẳng (thước mét) mà người bán vải sửu dụng, hoàn toàn không có ghi bất kì số liệu nào, mà chỉ gồm có 10 đoạn xanh, trắng xen kẽ nhau. theo em, thước có GHĐ và ĐCNN nào sau đây:
A. GHĐ 1m và ĐCNN 10cm
B. GHĐ 1m và ĐCNN 1 tấc
C. GHĐ 1,5m và ĐCNN 1cm
D. A và B đúng

Lời giải:
a. \(\lim\limits_{x\to 1+}(x^3+x+1)=3>0\)
\(\lim\limits_{x\to 1+}(x-1)=0\) và $x-1>0$ khi $x>1$
\(\Rightarrow \lim\limits_{x\to 1+}\frac{x^3+x+1}{x-1}=+\infty\)
b.
\(\lim\limits_{x\to -1+}(3x+2)=-1<0\)
\(\lim\limits_{x\to -1+}(x+1)=0\) và $x+1>0$ khi $x>-1$
\(\Rightarrow \lim\limits_{x\to -1+}\frac{3x+2}{x+1}=-\infty\)
c.
\(\lim\limits_{x\to 2-}(x-15)=-17<0\)
\(\lim\limits_{x\to 2-}(x-2)=0\) và $x-2<0$ khi $x<2$
\(\Rightarrow \lim\limits_{x\to 2-}\frac{x-15}{x-2}=+\infty\)
a)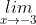
 =
=  = -4.
= -4.
b)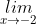
 =
= 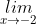
 =
= 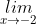 (2-x) = 4.
(2-x) = 4.
c)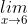
 =
= 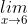

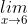
 =
= 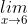
 =
=  .
.
=
d)
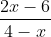 =
= 
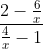 = -2.
= -2.
e)
 = 0 vì
= 0 vì  (x2 + 1) =
(x2 + 1) =  x2( 1 +
x2( 1 + 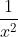 ) = +∞.
) = +∞.
f)
 =
= 
![This is the rendered form of the equation. You can not edit this directly. Right click...
</div>
<div class=]()